Java枚举算法怎么使用
想要使用枚举算法，首先要确定枚举对象、枚举范围和判定条件。逐一枚举可能的解，验证每个解是否是问题的解，千万不要漏掉任何一个可能正确的解。举个栗子百钱买百鸡问题：有一个人有一百块钱，打算买一百只鸡。到市场一看，大鸡三块钱一只，小鸡一块钱三只，不大不小的鸡两块钱一只。现在，请你编一程序，帮他计划一下，怎么样买法，才能刚好用一百块钱买一百只鸡？我们可以设公鸡为x，母鸡为y，小鸡为z，可以得出下列方程：x+y+ｚ＝100;5x+3y+z/3=100;现在只要穷举每一个公鸡的值，母鸡，小鸡的值就能通过公鸡的x表示出
想要使用枚举算法，首先要确定枚举对象、枚举范围和判定条件。逐一枚举可能的解，验证每个解是否是问题的解，千万不要漏掉任何一个可能正确的解。
举个栗子
百钱买百鸡问题：有一个人有一百块钱，打算买一百只鸡。到市场一看，大鸡三块钱一只，小鸡一块钱三只，不大不小的鸡两块钱一只。现在，请你编一程序，帮他计划一下，怎么样买法，才能刚好用一百块钱买一百只鸡？
我们可以设公鸡为x，母鸡为y，小鸡为z，可以得出下列方程：
x + y +ｚ＝100;
5x + 3y + z/3 = 100; 现在只要穷举每一个 公鸡的值，母鸡，小鸡的值 就能通过公鸡的 x 表示出来。
代码：
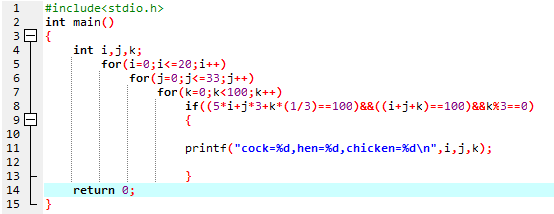
图中代码使用了三次for循环 时间复杂度（不知道的不用担心后期会专门出文章来讨论） 为O(N^3); 我们都喜欢一个程序简便，不消耗空间，短小精悍，看着高端的那种。下面介绍优化。
优化套路
虽然枚举是一种很暴利的算法，但是仍可以通过缩小枚举范围来提高解决问题的效率。同时也要避免重复枚举。
来看第二种方式：
x+y+z = 100 ①
5x+3y+z/3 = 100 ②
令②x3-① 可得
7x+4y = 100
=>y = 25-(7/4)x ③
又因为0 < y < 100 的自然数，则可令
x = 4k ④
将④代入③可得
=> y = 25-7k ⑤
将④⑤代入①可知
=> z = 75+3k ⑥
要保证 0 < x,y,z < 100 的话，k的取值范围只能是1,2,3
代码：
这个代码就达到了一层循环的基础，时间复杂度为 O（n）；
这个栗子介绍了枚举优化的一种套路就是减少枚举的变量。整个优化枚举的套路主要是有两个方面一个是减少枚举变量，一个是缩小枚举范围。
深入解析Java中局部变量未初始化编译报错与成员变量自动赋予默认值的机制差异，涵盖JVM内存分配、编译期确定性赋值检查与实际排查修复方案。
详细讲解在Java中获取当前系统时间并进行格式化输出的两种核心方案：基于Java 8全新日期时间API的DateTimeFormatter与传统遗留的SimpleDateFormat，包含完整代码示例、线程安全机制对比及生产选型建议。
深入解析Java中final变量与static final常量的定义、内存语义、初始化时机及合法赋值路径，涵盖编译期常量优化与实战避坑指南。
本文提供Java标准库HttpClient发起HTTP GET/POST请求并结合Jackson进行JSON数据反序列化与序列化的完整代码示例与工程实践指南。
详细分析Java递归调用出现StackOverflowError的原因，结合代码说明线程栈、栈帧和递归深度之间的关系，并介绍终止条件排查、迭代改写、减少栈帧开销以及通过-Xss调整JVM栈空间的方法。
针对Java中常见的NullPointerException（NPE），本文从堆栈日志定位、典型代码触发场景、具体修复代码对比到防御体系进行系统讲解，提供实用且易上手的排查与修复方案。
针对大数据工程场景，系统对比Java、Scala与Python在执行性能、生态结合、开发效率和维护成本上的核心差异，给出清晰的架构选型依据与落地方案。
火山引擎是字节跳动旗下企业级云与AI服务平台。聚焦大模型核心能力，依托字节自研豆包多模态大模型，凭借火山方舟一站式平台，提供模型精调、推理部署、智能应用搭建等全链路服务，结合高性能AI算力，助力各行业快速落地大模型数字化与智能化应用。
