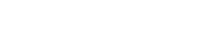本文提出的 Poseidon 在样本效率和准确率方面都表现出色。
偏微分方程（PDEs）被称为物理学的语言，因为它们可在广泛的时间和空间尺度上对各种各样的物理现象进行数学建模。常用的有限差分、有限元等数值方法通常用于近似或模拟偏微分方程。
然而，这些方法计算成本高昂，特别是对于多查询问题更是如此，因而人们设计了各种数据驱动的机器学习（ML）方法来模拟偏微分方程。其中，算子学习（operator learning）算法近年来受到越来越多的关注。
然而，现有的算法学习方法样本效率并不高，因为它们需要大量的训练样例才能以期望的准确率学习目标解算子（如图1所示）。这阻碍了算法学习的广泛应用，因为通过数值模拟或底层物理系统的测量来生成特定任务的训练数据非常昂贵。
研究者不禁提出，如何才能显著减少 PDE 学习所需的训练样本数量？
Poseidon正在大规模数据集上进行了预训练和评估。具体而言，他们在15项具有挑战性的下游任务上对Poseidon进行了评估，这些任务涉及线性和非线性、时间相关性和椭圆、抛物线、双曲线和混合型PDE。
结果表明，Poseidon 在样本效率和准确率方面都远远超过基线，展现出优异的性能。
Poseidon是一个非常好地地波化到预训练期间未见过的物理学问题。此外，Poseidon可以根据模型和数据大小进行扩展，无论是预训练还是下游任务。总结来看，本文展示了 Poseidon 的惊人能力，它能够在预训练期间从非常小的一组 PDE 中学习有效表达，从而很好地扩展到下游未见过和不相关的 PDE，证明了其作为有效通用 PDE 基础模型的潜力。
这些结果首次确定了PDE基础模型的可行性。这一基本问题，并为进一步开发和部署Poseidon作为高效的通用PDE基础模型铺平了道路。
最后，Poseidon 模型以及底层预训练和下游数据集都是开源的。
论文地址：https://arxiv.org/pdf/2405.19101
项目地址：https://github.com/camlab-ethz/poseidon
论文标题：Poseidon: Efficient Foundation Models for PDEs
方法介绍
问题描述：该研究将偏微分方程表示为：
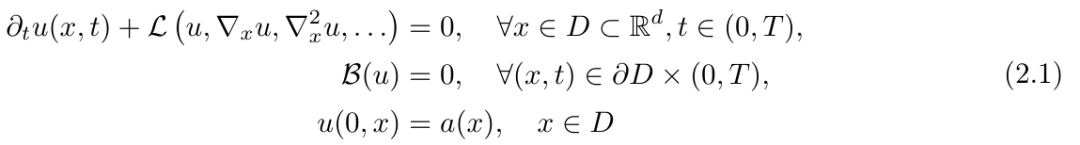
然后假设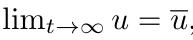
，可以得到与时间无关的 PDE 的解：
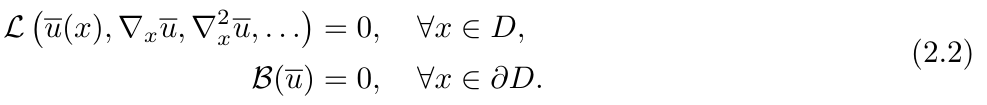
模型架构。Poseidon（图 1 和图 2）包括：i）可扩展的 Operator Transformer 或 scOT，这是一种具有（移位）窗口或 Swin 注意力机制的多尺度视觉 transformer，适用于算子学习；ii）一种新颖的 all2all 训练策略；iii）以及一个开源大型预训练数据集。
其中 scOT 是一种具有前置时间条件的分层多尺度视觉 transformer，用来处理前置时间 t 和函数空间值初始数据输入 a，以近似 PDE (2.1) 的解算子 S (t, a)。
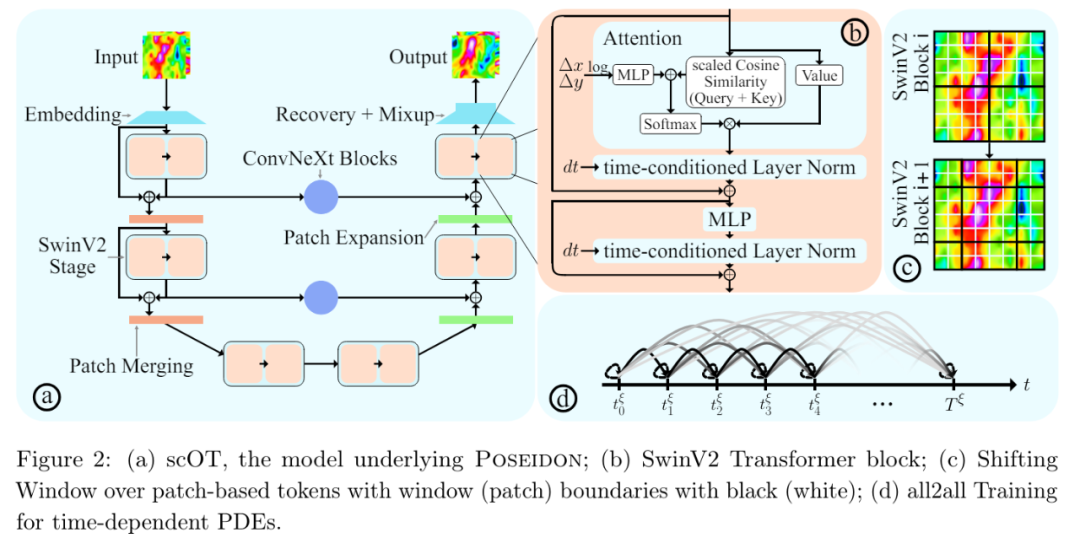
接着如图 2 (a) 所示，研究者通过 SwinV2 transformer 块对 patch 嵌入的输出进行处理，每个 transformer 块的结构表示为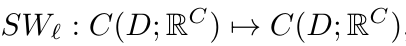
，得到：
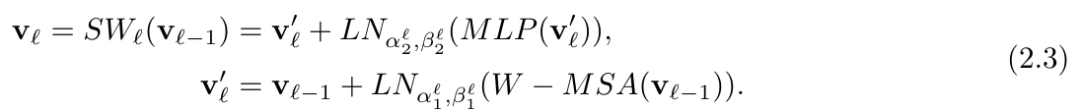
通过在 (2.3) 中引入前置时间条件层范数，该研究提出了一种时间调节策略。
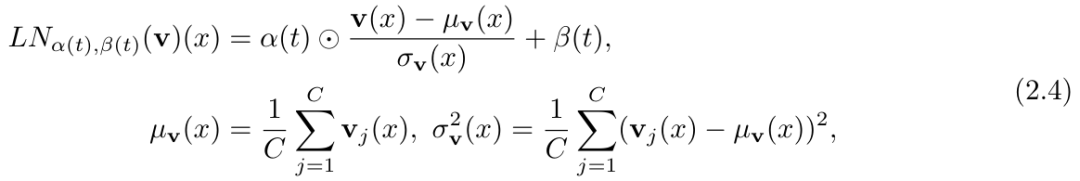
最后，如图 2 (a) 所示，SwinV2 transformer 块在 U-Net 类型的编码器 - 解码器架构中以层级多尺度方式排列，通过使用 patch 合并（下采样）和 patch 扩展（上采样）操作完成。
实验结果
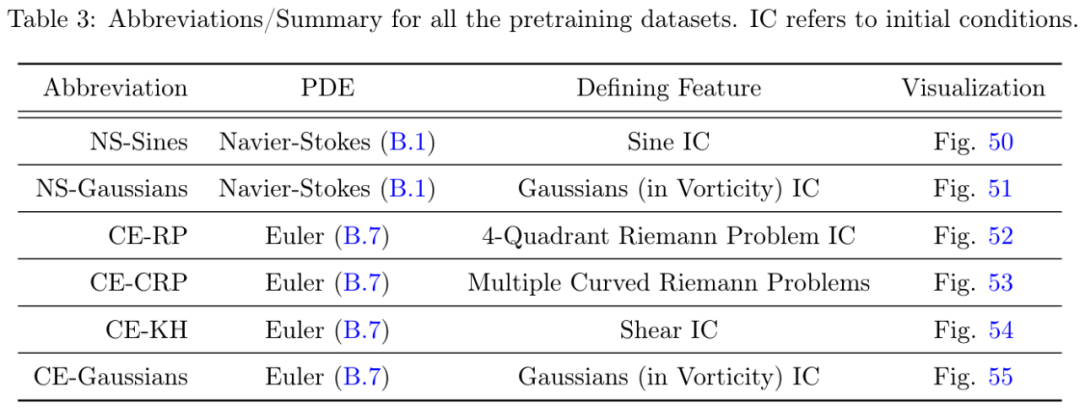
预训练数据：研究者提供了包含 6 个算子的数据集，详细信息如下所示。
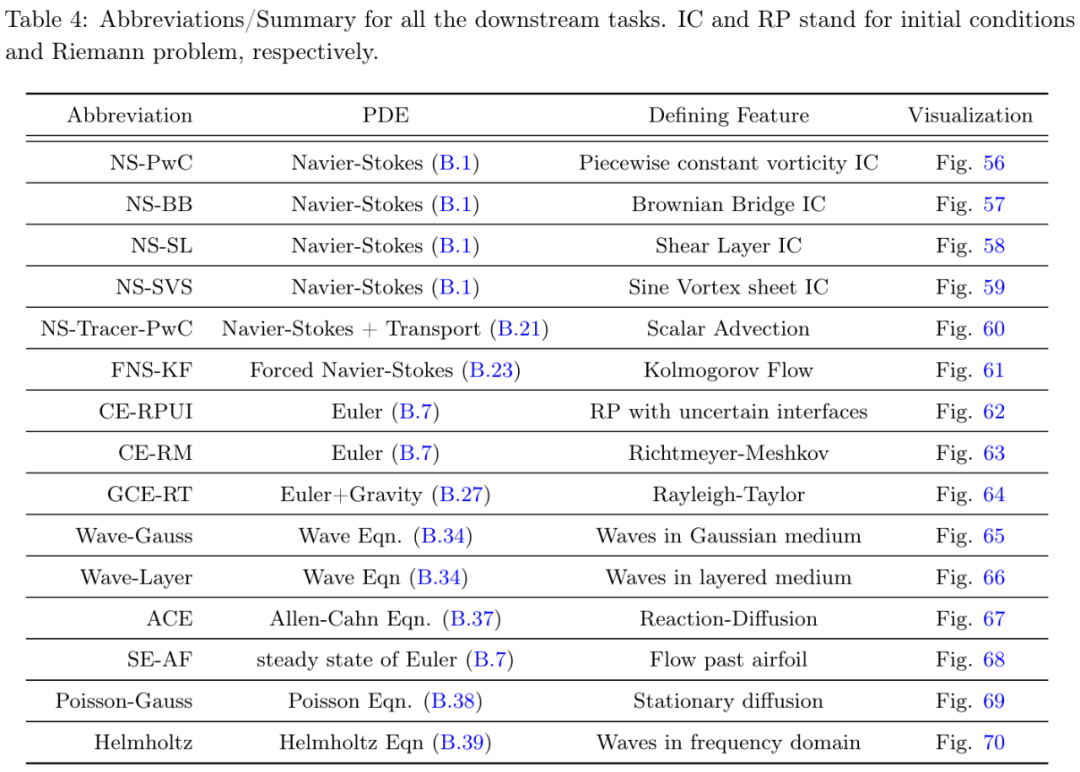
下游任务：研究者在 15 个具有挑战性的下游任务上进行了实验，如表 4 所示。
模型：本文考虑了三种不同的 Poseidon 模型：i) Poseidon-T ≈ 21M 个参数，ii) Poseidon-B ≈ 158M 个参数，iii) Poseidon-L ≈ 629M 个参数。
实验结果显示，Poseidon 在 15 个下游任务中都表现良好，明显优于 FNO（ Fourier Neural Operator ）（参考论文中的图 7 - 图 21，这里只展示图 7 ）。
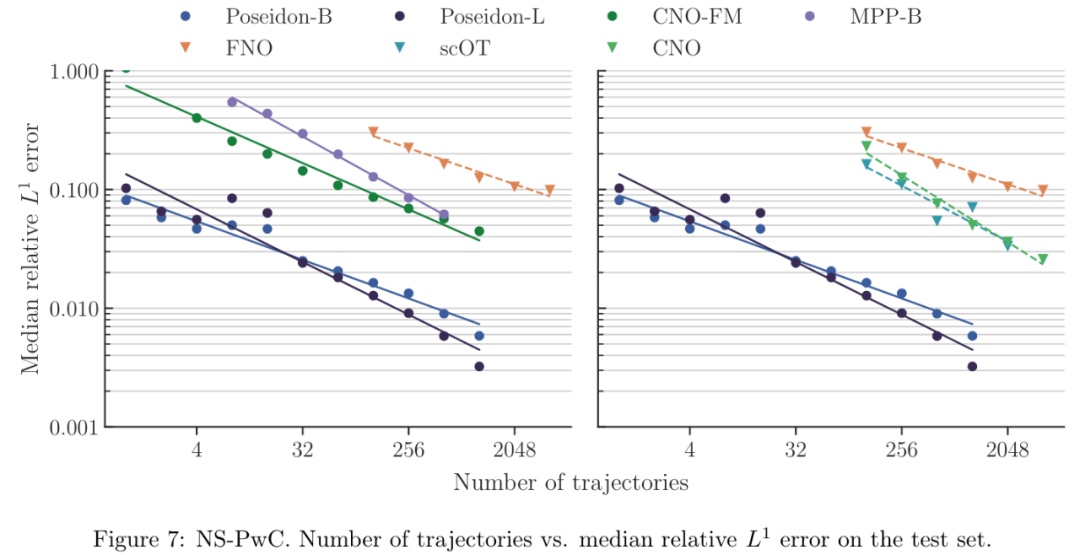
表 1 进一步支持了这一点。
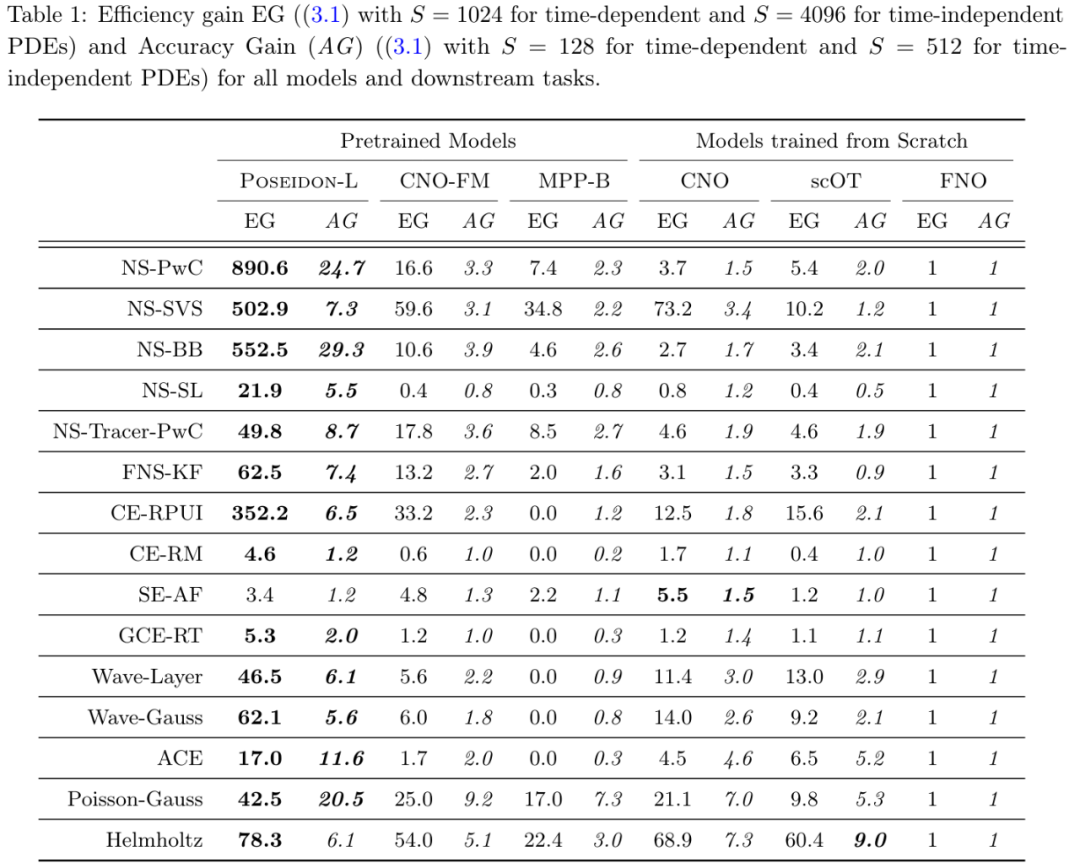
从表 9 可得，平均而言，Poseidon-L 仅需要 20 个样本即可达到 FNO 的 1024 个样本的误差，并且在 13 个（15 个）任务中，Poseidon-L 所需的样本比 FNO 少一个数量级。同样，从表 1 和表 9 中可以看到，对于相同数量的样本，Poseidon-L 的误差明显低于 FNO，增益范围从 10% 到 25 倍不等 ，此外，Poseidon 可以很好地泛化到未见过的物理任务。
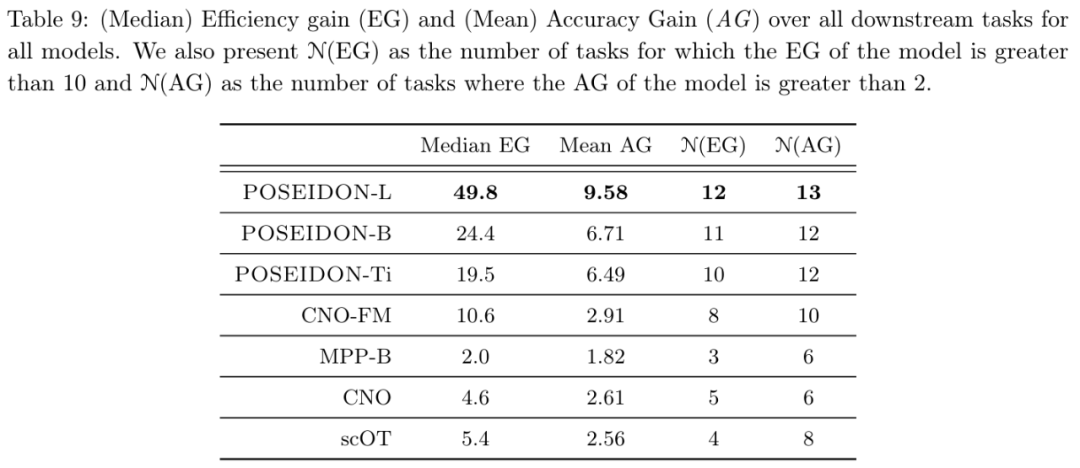
从表 1 和表 9 可以观察到，在 15 项下游任务中，Poseidon 在 14 项上的表现明显优于 CNO-FM。平均而言，CNO-FM 需要大约 100 个特定于任务的示例才能达到 FNO 的 1024 个样本的误差水平，而 Poseidon 只需要大约 20 个。由于 CNO-FM 和 Poseidon 已在完全相同的数据集上进行了预训练，因此这种性能差异很大程度上可以归因于架构差异，因为 CNO-FM 基于多尺度 CNN，而 Poseidon 的主干则是多尺度视觉 transformer。
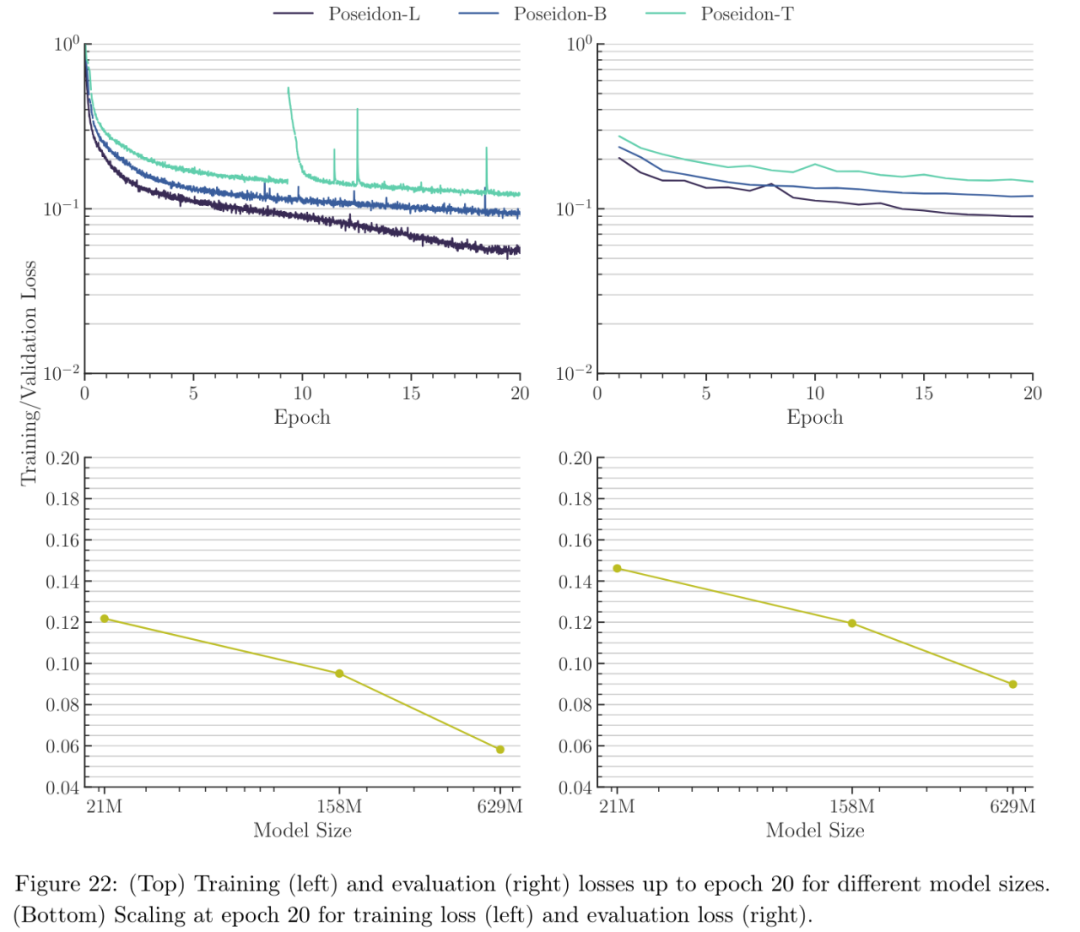
从图 22 可以看出，随着 Poseidon 模型大小的增加，预训练数据集上的训练和评估（验证）错误都明显减少。
了解更多结果，请参考原论文。
