反三角函数的定义域怎么
函数y=arcsin(2x+1)的定义域为:[-1,0]
计算过程如下:
设t=2x+1
∵反正弦函数y=arcsint的定义域为[-1,1]
∴解不等式-1≤2x+1≤1,可得x∈[-1,0]
所以函数的定义域为:[-1,0]
扩展资料:
反正弦arcsin x,反余弦arccos x,反正切arctan x,反余切arccot x,反正割arcsec x,反余割arccsc x这些函数的统称,各自表示其反正弦、反余弦、反正切、反余切 ,反正割,反余割为x的角。
反余弦函数y=arccos x的主值限在0≤y≤π;反正切函数y=arctan x的主值限在-π/2 找到一个单调区间,此区间即是烦函数的定义域。 把函数看作方程: y=f(x) 解方程,出x用y标识的表达式,x=f^(-1)(y) 将x,y互换即得反函数表达式: y=f^(-1)(x) 例如: y=3x+5的反函数,函数在(-∞, +∞)内单调,值域为:(-∞, +∞) ∴ 所以反函数的定义域为:(-∞, +∞),值域为:(-∞, +∞) 由 y=3x+5 解得:x=1/3*y-5/3 ∴ 反函数为: y=1/3*x-5/3 x∈(-∞, +∞) 例如 y=x^2,x=正负根号y,则f(x)的反函数是正负根号x,完后注意定义域和值域,反函数的定义域就是原函数的值域,反函数的值域就是原函数的定义域。 扩展资料: 一般来说,设函数y=f(x)(x∈A)的值域是C,若找得到一个函数g(y)在每一处g(y)都等于x,这样的函数x= g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数,记作y=f^(-1)(x) 。反函数y=f ^(-1)(x)的定义域、值域分别是函数y=f(x)的值域、定义域。最具有代表性的反函数就是对数函数与指数函数。 一般地,如果x与y关于某种对应关系f(x)相对应,y=f(x),则y=f(x)的反函数为x=f (y)或者y=f﹣¹(x)。存在反函数(默认为单值函数)的条件是原函数必须是一一对应的(不一定是整个数域内的)。注意:上标"−1"指的并不是幂。 在证明这个定理之前先说明函数的严格单调性。 设y=f(x)的定义域为D,值域为f(D)。如果对D中任意两点x1和x2,当x1y2,则称y=f(x)在D上严格单调递减。 证明:设f在D上严格单增,对任一y∈f(D),有x∈D使f(x)=y。 而由于f的严格单增性,对D中任一x'x,都有y''>y。总之能使f(x)=y的x只有一个,根据反函数的定义,f存在反函数f-1。 任取f(D)中的两点y1和y2,设y1 若此时x1≥x2,根据f的严格单增性,有y1≥y2,这和我们假设的y1 因此x1 如果f在D上严格单减,证明类似。 参考资料:搜狗百科---反函数 反函数为: y = 2sin(x/3),定义域为: [-3π/2,3π/2] y = 3arcsin(x/2) y/3 = arcsin(x/2) sin(y/3) = x/2 2sin(y/3)=x 反函数为: y = 2sin(x/3) 定义域为: [-3π/2,3π/2] 扩展资料 反函数的性质: (1)函数存在反函数的充要条件是,函数的定义域与值域是一一映射; (2)一个函数与它的反函数在相应区间上单调性一致; (3)大部分偶函数不存在反函数(当函数y=f(x), 定义域是{0} 且 f(x)=C (其中C是常数),则函数f(x)是偶函数且有反函数,其反函数的定义域是{C},值域为{0} )。 (4)一段连续的函数的单调性在对应区间内具有一致性; (5)严增(减)的函数一定有严格增(减)的反函数; (6)反函数是相互的且具有唯一性。如何反函数的定义域
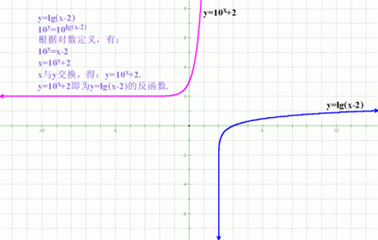
反三角函数的反函数详细解