揭秘Transformer数学原理，全新版本让你大开眼界
近日，arxiv上发布了一篇论文，对Transformer的数学原理进行全新解读，内容很长，知识很多，十二分建议阅读原文。2017年，Vaswani等人发表的《Attentionisallyouneed》成为神经网络架构发展的一个重要里程碑。这篇论文的核心贡献是自注意机制，这是Transformers区别于传统架构的创新之处，在其卓越的实用性能中发挥了重要作用。事实上，这一创新已成为计算机视觉和自然语言处理等领域人工智能进步的关键催化剂，同时在大语言模型的出现中也起到了关键作用。因此，了解Transfor
近日，arxiv 上发布了一篇论文，对 Transformer 的数学原理进行全新解读，内容很长，知识很多，十二分建议阅读原文。
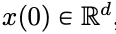在时间间隔 （0，T） 上会按照给定的时变速度场 
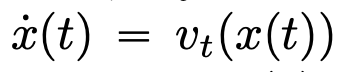进行演化。因此，DNN 可以看作是从一个 
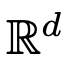到另一个
的流映射（Flow Map）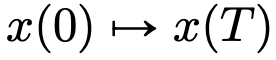
。即使在经典 DNN 架构限制下的速度场
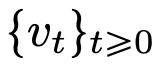中，流映射之间也具有很强的相似性。
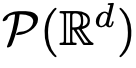上的流映射，即 d 维概率测度空间（the space of probability measures）间的映射。为了实现这种在度量空间间进行转换的流映射，Transformers 需要建立了一个平均场相互作用的粒子系统（mean-field interacting particle system.）。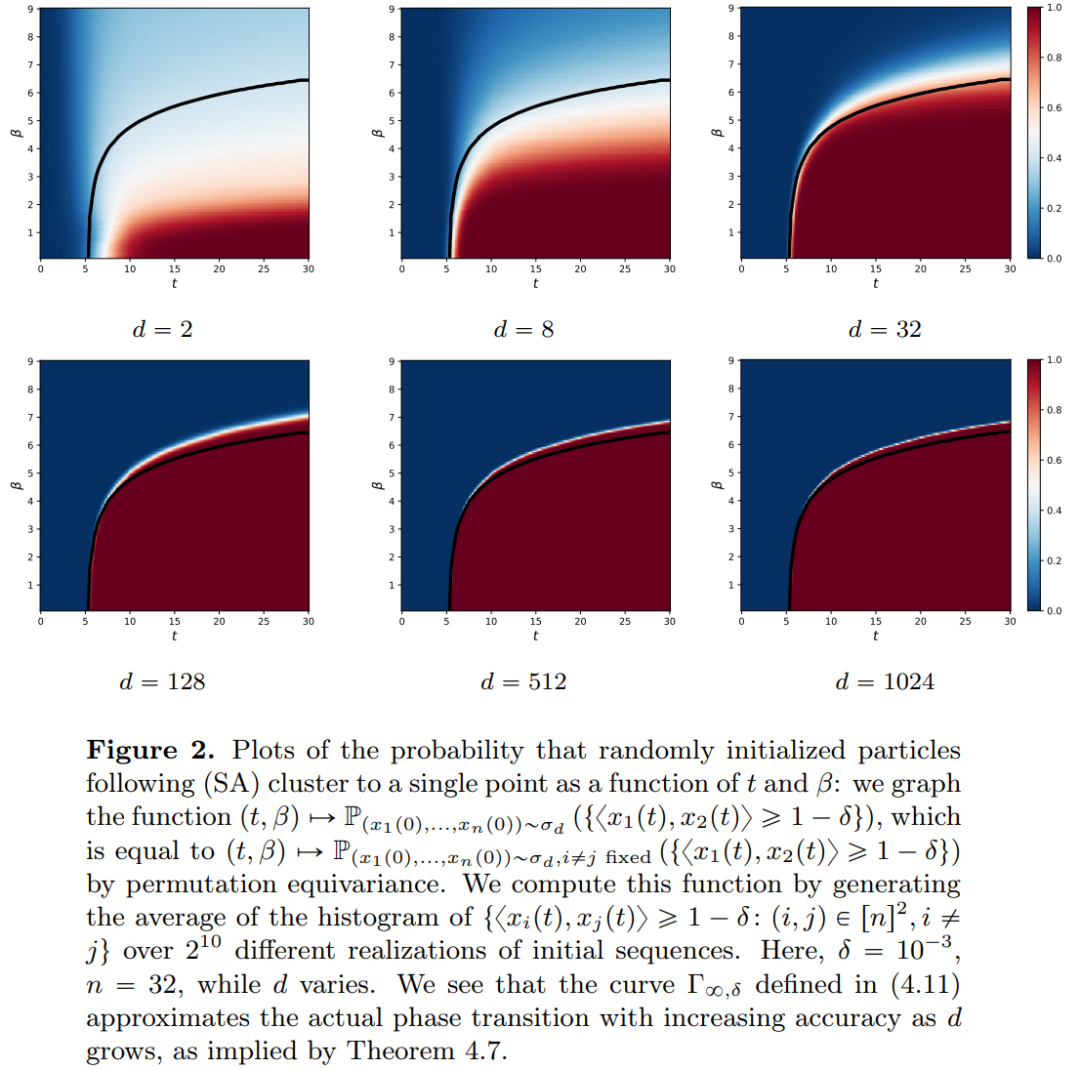
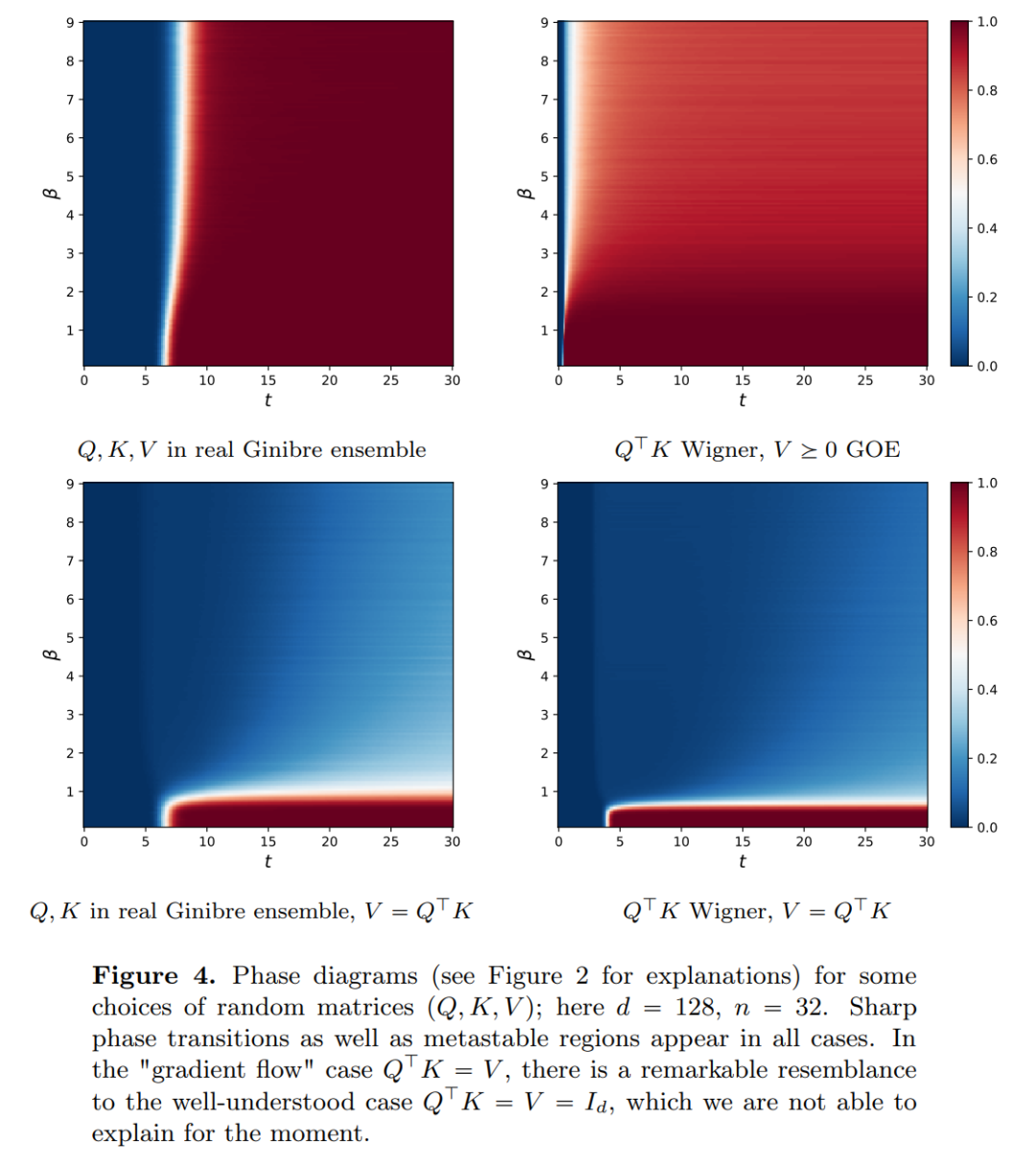
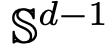的空间内部，而自注意力机制则是通过经验度量实现粒子之间的非线性耦合。反过来，经验度量根据连续性偏微分方程进行演化。本文还为自注意引入了一个更简单好用的替代模型，一个能量函数的 Wasserstein 梯度流，而能量函数在球面上点的最优配置已经有成熟的研究方法。
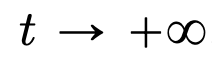时聚成一个点。研究者对粒子集群收缩率的精确描述对这一结果进行了补充说明。具体来说，研究者绘制了所有粒子间距离的直方图，以及所有粒子快要完成聚类的时间点（见原文第 4 节）。研究者还在不假设维数 d 较大的情况下就得到了聚类结果（见原文第 5 节）。
比特现金（BCH）的未来发展前景看好。凭借其可扩展性、支付采用、价值存储、智能合约和坚实的社区支持，比特现金有望在多个领域取得显著发展，成为一种多功能且广泛使用的加密货币。
ACH 总共发行了 10 亿枚，用于支付网关费用、治理投票和质押奖励。ACH 基于 BEP-20 标准，采用 PoS 机制，可通过私募、公募和生态系统分配获取，其价值受服务需求、实用性和市场趋势影响，可在币安、火币等交易所购买。
Coinbase Pro 设置步骤：下载并安装软件后，打开并登录，点击右上角齿轮图标进入“首选项”。在首选项中，你可以调整界面、安全、通知、交易和API设置，完成后点击“保存”按钮确认更改。
IoTeX、DePHY和peaq是构建物联网生态系统的关键基础设施。IoTeX提供去中心化网络，确保物联网交易和数据的安全性。DePHY利用区块链技术实现频谱共享和自治管理。peaq促进设备间的数据标准化和共享。通过这些基础设施的协同作用，物联网生态系统实现了去中心化、安全、互操作性和自治，充分释放了物联网的潜力。
Windows 10 是一款微软推出的经典操作系统，拥有硬件兼容性与多任务处理能力。它更偏向把系统状态查看和常用调节动作放在一起，适合需要持续观察和微调设备状态的场景。
极度公式是一款跨平台专业LaTeX公式识别编辑软件，支持OCR公式识别和多平台编辑。和使用说明，避免使用，享受完整功能与稳定支持。做扫描整理、文字提取和表格转换时，它能把识别后的处理步骤接得更顺，资料录入这类场景会省下不少时间。
