逻辑函数卡诺图原理
 发布于2025-01-23 阅读(0)
发布于2025-01-23 阅读(0)
扫一扫,手机访问

逻辑函数卡若图
卡诺图化简逻辑函数方法
在卡诺图中,相邻的最小项在逻辑上也是相邻的。逻辑相邻的意思是,这两个最小项除了一个变量的形式不同为互反变量外,其他都是相同的。因此,这些相邻的最小项可以合并成一个与项,并消去其中的互反变量。
①哪些方格相邻
在卡诺图中,相邻有三种情况:
相连:二个小方格互相紧挨着,不管从那个方向,上下还是左右;
相对:任意一行或一列的两头的小方格;
相重:对折起来位置重合的小方格。
②合并的原则
凡是相邻的最小项均可以合并,那么合并如何进行,合并的结果又如何呢?
(1)二个最小项合并,消去一个互反变量,保留公共变量;
(2)四个最小项合并,消去二个互反变量,保留公共变量;
(3)八个最小项合并,消去三个互反变量,保留公共变量。
一般地说,2^n个最小项合并,可以消去n个变量。当卡诺图中全部最小项均为“1”时,整个卡诺图就是一个大的相邻区域,可消去全部n个互反变量,使函数值恒为“1”。
画圈应遵循以下原则:
(1)取大不取小,圈越大,消去的变量越多,与项越简单,能画入大圈就不画入小圈;
(2)圈数越少,化简后的与项就越少;
(3)一个最小项可以重复使用,即只要需要,一个方格可以同时被多圈所圈;
(4)一个圈中的小方格至少有一个小方格不为其它圈所圈;
(5)画圈必须覆盖完每一个填“1”方格为止。
将每个圈中互反变量消去,保留公共变量,所得对应的与项再逻辑“或”起来,得到最简与或表达式。
怎么用WORD画卡诺图
利用卡诺图化简逻辑函数的步骤如下:
第一步:将逻辑函数变换为最小项之和的形式
第二步:画出表示该逻辑函数的卡诺图
第三步:找出可以合并的最小项并画出合并圈
第四步:写出最简的与-或表达式
在利用卡诺图化简逻辑函数时,关键在于画合并圈。合并圈画得不同,逻辑函数的表达式也不相同。因此画合并圈时应注意以下几点:
①首先要找出孤立的1方格并画圈。
②合并圈的范围越大越好,但必须包含(i=0,1,2,3…)个1方格,这样能消去的变量就越多。
③合并圈的个数越少越好,因为合并圈的个数与化简结果中乘积项的个数相对应,圈数越少意味着与-或表达式中与项越少。
④每个合并圈中至少要包含一个其它合并圈中没有包含的1方格,这样才能保证这个合并圈不是多余的。
⑤卡诺图中所有的1方格至少要被圈一次,不能有漏画的1方格。
这样,把每个合并圈相对应的与项“加”起来,就得到最简的与-或表达式。
同理的方法,只要合并圈改为针对卡诺图中的0方格进行,找出可合并的最大项,就可得到逻辑函数的最简或-与表达式。
合并最大项的规律与合并最小项的规律基本一致。不同之处在于,合并最大项时必须找出0方格的相邻性。每个合并圈可由(i=0,1,2,3…)个0方格构成,每个合并圈对应于一个或项,该或项由圈内取值不变的变量相或来构成,其中取值为0的对应原变量,取值为1的对应反变量。然后将每个合并圈对应的或项进行相与,便得到最简的或-与表达式
产品推荐
-

售后无忧
立即购买>- DAEMON Tools Lite 10【序列号终身授权 + 中文版 + Win】
-
¥150.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Ultra 5【序列号终身授权 + 中文版 + Win】
-
¥198.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Pro 8【序列号终身授权 + 中文版 + Win】
-
¥189.00
office旗舰店
-

售后无忧
立即购买>- CorelDRAW X8 简体中文【标准版 + Win】
-
¥1788.00
office旗舰店
-
 正版软件
正版软件
- 哪种软件可用于调试飞控?
- 调试飞控用什么软件下载mwc的飞控源码,网盘里有,这是我定制过的,适用于我们的小飞机,其他来源的可能不适合。2.插上ftdi下载器,具体步骤如下所示(1)将FTDI下载器接口用杜邦线引出,如图用排针挨个链接好,顺序不用调。下载器的跳线帽接在5v上下载器的CTS接飞机接口的GND上(3)安装FTDI驱动程序(网盘里有)(4)3.打开multiwii.ino4.选择板子类型为5V,16MHz5.这里选择你下载器的串口6.电机下载按钮,开始下载程序7.上位机调试飞控,下载网盘里的上位机调试软件,8.根据电脑操作
- 12分钟前 0
-
正版软件
- 转换其他文件格式为TmP文件的简单方法
- 如何将其他文件转换为TMP文件格式?近年来,随着科技的进步和网络的普及,我们经常需要将不同格式的文件转换为其他格式以适应不同的需求。一个常见的需求就是将其他文件转换为TMP文件格式。TMP文件格式一般用于临时存储临时数据,具有临时性和可编辑性的特点。那么,如何实现这一转换呢?下面就来介绍一些方法。方法一:使用专业文件转换工具目前市面上有许多专业的文件转换工具
- 27分钟前 文件转换 转换文件格式 TmP文件格式 0
-
 正版软件
正版软件
- 云电脑游玩逆水寒的选择是否可信?(云电脑游玩逆战需要怎样付费?)
- 云电脑玩逆水寒能靠谱吗回答如下:云电脑可以在一定程度上提供稳定的游戏体验,但是具体靠不靠谱还需要考虑多方面因素,比如网络稳定性、电脑配置、游戏本身的优化程度等等。所以不能保证云电脑玩逆水寒一定靠谱,需要根据具体情况来决定。可以靠谱地玩逆水寒。原因是云电脑的优点在于可以提供稳定的网络和计算资源,而逆水寒是一款网游,对网络和计算资源的要求较高。通过云电脑的方式可以有效解决这些问题,确保游戏的流畅性和稳定性。另外,云电脑还可以提供更高的游戏画质和更快捷的游戏启动速度,能够提升玩家的游戏体验。此外,云电脑还支持多
- 42分钟前 电脑 云 怎么 逆水寒 玩 能 靠 谱吗 玩逆 战 0
-
 正版软件
正版软件
- 解决win10心灵终结无法启动的问题
- 心灵终结是红色警戒2的又一续作,吸引了很多的忠实玩家来重温经典,可是很多小伙伴下载了正要玩的时候都遇到了打不开的情况,下面就给你们带来了解决方法一起看看吧win10心灵终结打不开怎么办:方法一:1、右击桌面的游戏快捷方式,点击“属性”。2、随后点击“兼容性”,选择“WindowsXP(ServicePack3)”。点击“确定”即可。方法二:1、进入游戏的根目录找到“ra2.ini”文件双击打开。2、在“Video”中加入代码:AllowHiResModes=yesVideoBackBuffer=noAll
- 57分钟前 win 解决方法。 心灵终结 0
-
 正版软件
正版软件
- 如何使用C语言从声卡读取音频数据并进行传输
- 请问大家如何用C从声卡读取音频数据并发送引用:usingnamespaceMicrosoft;usingnamespaceMicrosoft::DirectX;usingnamespaceMicrosoft::DirectX::DirectSound;usingnamespaceMicrosoft::DirectX::AudioVideoPlayback;初始化:Device设备=newDevice();设备.SetCooperativeLevel(this,CooperativeLevel.Normal
- 1小时前 21:30 vc声卡读数据 0
最新发布
-
 1
1
- KeyShot支持的文件格式一览
- 1687天前
-
 2
2
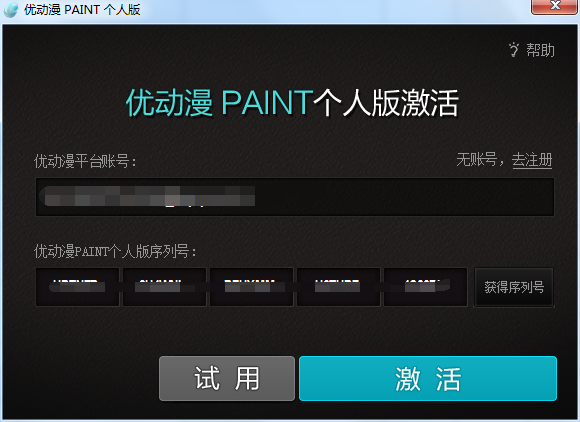
- 优动漫PAINT试用版和完整版区别介绍
- 1727天前
-
 3
3
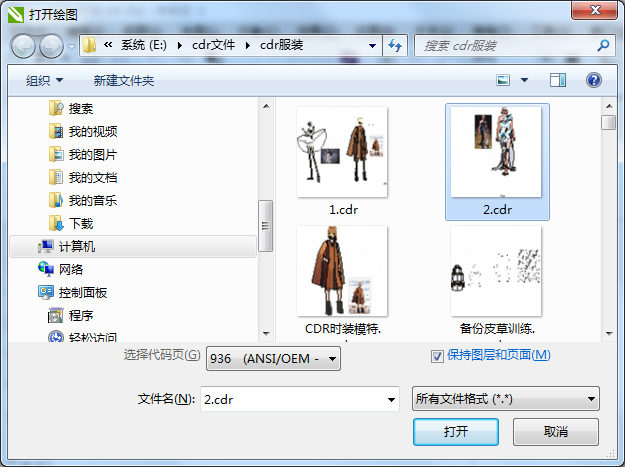
- CDR高版本转换为低版本
- 1872天前
-
 4
4
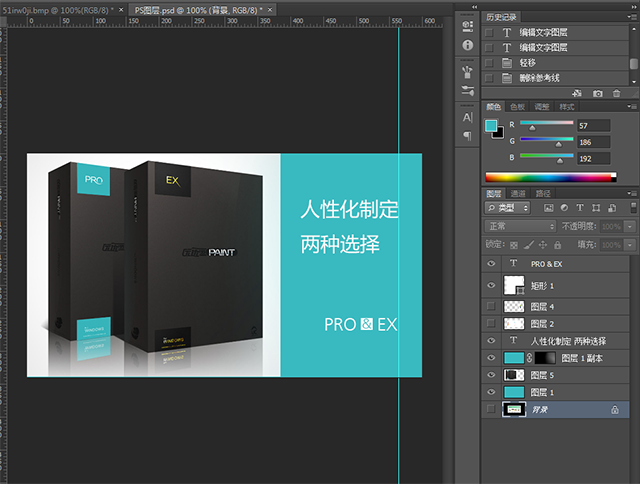
- 优动漫导入ps图层的方法教程
- 1727天前
-
 5
5
- ZBrush雕刻衣服以及调整方法教程
- 1723天前
-
 6
6
- 修改Xshell默认存储路径的方法教程
- 1738天前
-
 7
7
- Overture设置一个音轨两个声部的操作教程
- 1716天前
-
 8
8
- PhotoZoom Pro功能和系统要求简介
- 1892天前
-
 9
9
- CorelDRAW添加移动和关闭调色板操作方法
- 1765天前
相关推荐
热门关注
-

- Xshell 6 简体中文
- ¥899.00-¥1149.00
-

- DaVinci Resolve Studio 16 简体中文
- ¥2550.00-¥2550.00
-

- Camtasia 2019 简体中文
- ¥689.00-¥689.00
-

- Luminar 3 简体中文
- ¥288.00-¥288.00
-

- Apowersoft 录屏王 简体中文
- ¥129.00-¥339.00