推导一元二次方程的公式法的方法是什么?
 发布于2025-01-31 阅读(0)
发布于2025-01-31 阅读(0)
扫一扫,手机访问
一元二次方程的公式法怎么推导的
ax²+bx+c=0
两边同时除以a
x²+(bx/a)+c/a=0
两边加上配方项(b/2a)²
x²+(bx/a)+(b/2a)²+c/a=(b/2a)²
左边是配好的完全平方式,并把c/a移到右边
(x+(b/2a))²=(b/2a)²-(c/a)
右边通分,然后两边开方得
|x+(b/2a)|=[根号(b²-4ac)]/(2a)
去掉绝对值符号得
x+(b/2a)=±[根号(b²-4ac)]/(2a)
把(b/2a)移到右边去
x=[-b±根号(b²-4ac)]/(2a)
当b²-4ac>0时,方程有两个不同的根
当b²-4ac=0时,方程有1个根
当b²-4ac<0时,方程有没有实根
一元二次方程的公式是怎么样的
一般来说,一元二次方程的解法有:(注:以下 ^ 是平方的意思。)
一、直接开平方法。如:x^2-4=0
解:x^2=4
x=±2(因为x是4的平方根)
∴x1=2,x2=-2
二、配方法。如:x^2-4x+3=0
解:x^2-4x=-3
配方,得(配一次项系数一半的平方)
x^2-2*2*x+2^2=-3+2^2(方程两边同时加上2^2,原式的值不变)
(x-2)^2=1【方程左边完全平方公式得到(x-2)^2】
x-2=±1
x=±1+2
∴x1=1,x2=3
三、公式法。(公式法的公式是由配方法推导来的)
-b±∫b^2-4ac(-b加减后面是 根号下b^2-4ac)
公式为:x=-------------------------------------------(用中
2a
文吧,希望你能理解:2a分之-b±根号下b^2-4ac)
利用公式法首先要明确什么是a、b、c。
其实它们就是最标准的二元一次方程的形式:ax^2+bx+c=0
△=b2-4ac称为该方程的根的判别式。
当b2-4ac>0时,方程有两个不相等的实数根;
当b2-4ac=时,方程有两个相等的实数根;
当b2-4ac<0时,方程没有实数根。
有些时候,做到b2-4ac<0时,需要讨论△,因为根号下的数字是非负数,<0也就没有实数根,也就没有做的意义了。
a代表二次项的系数,b代表着一次项系数,c是常数项
注意:用公式法解一元二次方程时首先要化成一般形式,也就是ax^2+bx+c=0的形式,然后才能做。
解题时按照上面的公式,把数字带入计算就OK了。这对任何一元二次方程都可以操作。
一元二次方程的解法公式法的推导
首先当a不等于0时方程:ax^2+bx+c=0才是一元二次方程
1.公式法:Δ=b²-4ac,Δx=【-b±根号下(b²-4ac)】÷2a(Δ=0时x只有一个)
2.配方法:可将方程化为[x-(-b/2a)]²=(b²-4ac)/4a²
可解出:x=【-b±根号下(b²-4ac)】÷2a(公式法就是由此得出的)
3.直接开平方法与配方法相似
4.因式分解法:核心当然是因式分解了看一下这个方程
(Ax+C)(Bx+D)=0,展开得ABx²+(AD+BC)+CD=0与一元二次方程ax^2+bx+c=0对比得a=AB,b=AD+BC,c=CD。所谓因式分解也只不过是找到A,B,C,D这四个数而已
举几个例子吧
例1: x²-5x+6=0
解:(x-2)(x-3)=0,x1=2,x2=3
例2: 3x²-17x+10=0
解: (3x-2)(x-5)=0,x1=2/3,x2=5
因式分解法又名十字相乘法原因看下面就知道了
ABx²+(AD+BC)+CD=0
Ax
C
↖↗
↙↘
Bx
D (A,B,C,D不一定都是正数)
解方程时因选择适当的方法
下面几个练习题可以试试
1.x²-6x+9=0
2.4x²+4x+1=0
3.x²-12x+35=0
4.x²-x-6=0
5.4x²+12x+9=0
6.3x²-13x+12=0
一元二次方程根公式详细的推导过程
一元二次方程根公式详细的推导过程:
一元二次方程的根公式是由配方法推导来的,那么由ax^2+bx+c(一元二次方程的基本形式)推导根公式的详细过程如下,
1、ax^2+bx+c=0(a≠0,^2表示平方),等式两边都除以a,得x^2+bx/a+c/a=0,
2、移项得x^2+bx/a=-c/a,方程两边都加上一次项系数b/a的一半的平方,即方程两边都加上b^2/4a^2,
3、配方得 x^2+bx/a+b^2/4a^2=b^2/4a^2-c/a,即 (x+b/2a)^2=(b^2-4ac)/4a,
4、开根后得x+b/2a=±[√(b^2-4ac)]/2a (√表示根号),最终可得x=[-b±√(b^2-4ac)]/2a。
一、一元二次方程根公式
1、
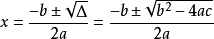
2、公式描述:一元二次方程形式:ax2+bx+c=0(a≠0,且a,b,c是常数)。
3、满足条件:
(1)是整式方程,即等号两边都是整式,方程中如果有分母;且未知数在分母上,那么这个方程就是分式方程,不是一元二次方程,方程中如果有根号,且未知数在根号内,那么这个方程也不是一元二次方程(是无理方程)。
(2)只含有一个未知数。
(3)未知数项的最高次数是2。
产品推荐
-

售后无忧
立即购买>- DAEMON Tools Lite 10【序列号终身授权 + 中文版 + Win】
-
¥150.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Ultra 5【序列号终身授权 + 中文版 + Win】
-
¥198.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Pro 8【序列号终身授权 + 中文版 + Win】
-
¥189.00
office旗舰店
-

售后无忧
立即购买>- CorelDRAW X8 简体中文【标准版 + Win】
-
¥1788.00
office旗舰店
-
 正版软件
正版软件
- 如何在win10锁屏上设置天气小工具
- 在最新版本的win10更新系统里面,为软件也改进了锁屏方面的使用体验,用户可以在电脑的锁屏界面上设置一些你喜欢的天气小部件,具体的方法如下,大家可以跟着步骤来操作。win10如何在锁屏上启用天气小部件1、点击后面的蓝色链接进入到页面然后下载“vivetool”工具,然后解压缩软件,记住你解压出来的文件路径。2、输入搜索cmd3、找到命令提示符然后右键“以管理员身份运行”3、使用cd命令输入你刚刚解压的那个软件的路径,比如说:cdC:\ProgramFiles(x86)\ViVeTool-v0.3.2”然后
- 4分钟前 锁屏 win10 天气小部件 0
-
 正版软件
正版软件
- Win7蓝牙设备添加指南
- win7系统中连接蓝牙设备是需要用户在设置中进行添加的,没有win10系统那么简单就可以连接的。这里小编为大家讲解win7添加蓝牙设备教程,希望对大家有帮助。win7添加蓝牙设备:1、在Windows7系统中打开控制面板,搜索Bluetooth。2、搜索到点击添加Bluetooth设备。3、点击添加以后蓝牙会自动搜索蓝牙设备,需要把蓝牙设备靠近电脑;4、在扫描后能够看见自己的蓝牙设备,选择要连接的蓝色设备添加连接。5、最后窗口显示此设备已成功添加到此计算机。
- 19分钟前 win 添加 蓝牙设备 0
-
 正版软件
正版软件
- 函数f(x)经过点A(2, 2^34 * 2^25 * 2^4)
- 一、已知函数fx=x^34x^2+5x4经过点A(2,2)的曲线,fx的切线方程?要求曲线在点A(2,2)的切线方程,需要进行以下步骤:1.求导:计算函数fx的导数,即fx',这将给出曲线在任意点的斜率。2.代入点A:将x值为2代入导数fx',得到在点A的切线的斜率。3.切线方程:利用点斜式或一般式等方法,将得到的斜率和点A(2,2)代入,得到切线方程。例如,如果导数为fx',在点A(2,2)的切线方程可以表示为y=fx'(2)(x-2)+2。二、函数fx=x^2+bx+c
- 34分钟前 0
-
 正版软件
正版软件
- 获取MFC对话框客户区鼠标点击位置坐标的具体代码
- MFC中如何得到对话框客户区中鼠标点下位置的坐标具体代码//在对话窗标题处实时显示客户区内鼠标的坐标voidCTestDlg::OnMouseMove(UINTnFlags,CPointpoint){//TODO:Addyourmessagehandlercodehereand/orcalldefaultCStringstr;str.Format("X:%dY:%d",point.x,point.y);//格式化鼠标坐标点信息并保存到CString型变量str中SetWindowText(str);//更
- 49分钟前 0
-
 正版软件
正版软件
- 修改数据库记录的值在VB中的实现方法
- VB怎么样修改数据库中记录的值楼上的道友的方法中:sSQL="updatetablesetfield=20"要改为:sSQL="updatetablesetfield1=20,...,field2=20whereid=3"但是如果你的数据库中没有记录3就会出错。还有一种方法,用recordset来处理:dimcnasnewadodb.connectiondimrsasnewadodb.recordsetrs.open"select*from数据库whereid=3",adOpenDynamic,adLoc
- 1小时前 06:40 0
最新发布
-
 1
1
- KeyShot支持的文件格式一览
- 1694天前
-
 2
2
- 优动漫PAINT试用版和完整版区别介绍
- 1735天前
-
 3
3
- CDR高版本转换为低版本
- 1880天前
-
 4
4
- 优动漫导入ps图层的方法教程
- 1734天前
-
 5
5
- ZBrush雕刻衣服以及调整方法教程
- 1730天前
-
 6
6
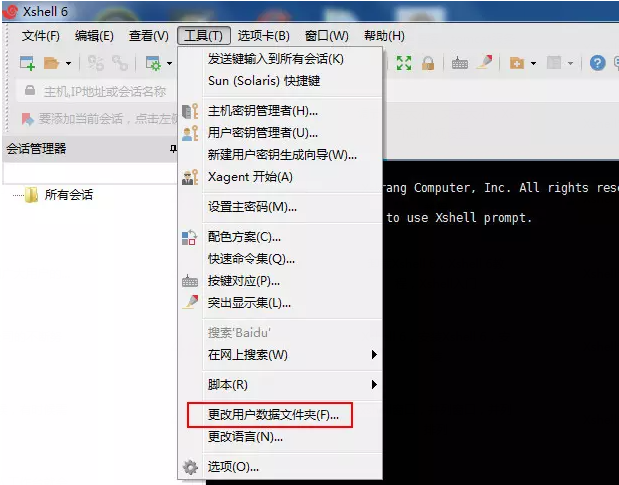
- 修改Xshell默认存储路径的方法教程
- 1746天前
-
 7
7
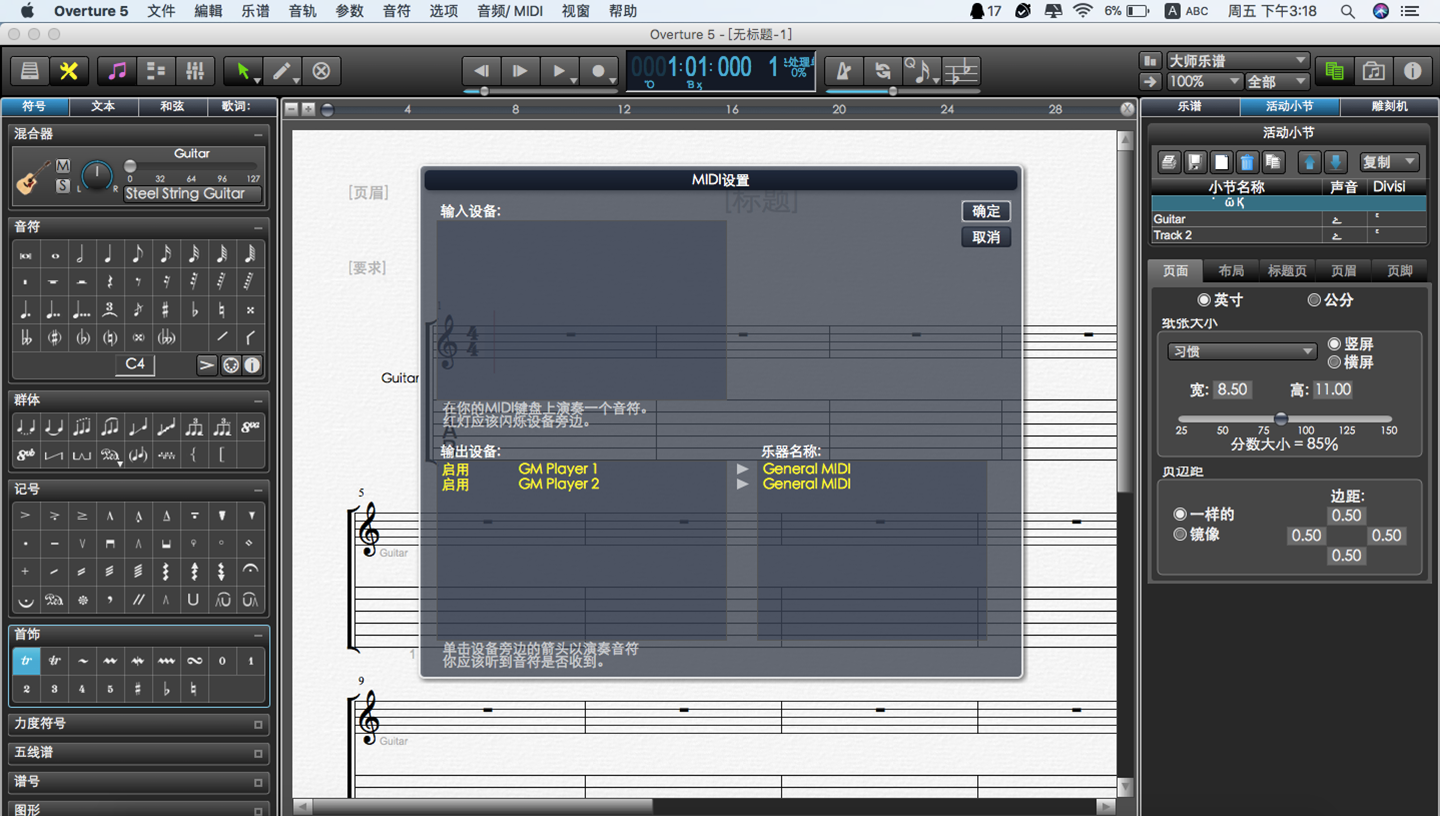
- Overture设置一个音轨两个声部的操作教程
- 1724天前
-
 8
8
- PhotoZoom Pro功能和系统要求简介
- 1900天前
-
 9
9
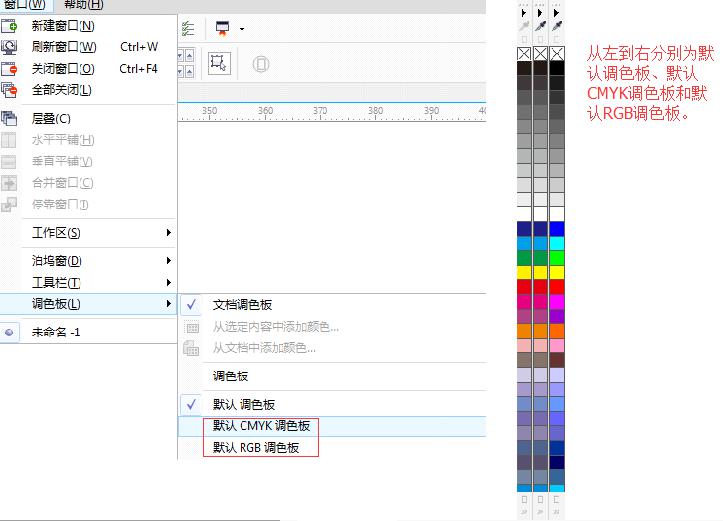
- CorelDRAW添加移动和关闭调色板操作方法
- 1773天前
相关推荐
热门关注
-

- Xshell 6 简体中文
- ¥899.00-¥1149.00
-

- DaVinci Resolve Studio 16 简体中文
- ¥2550.00-¥2550.00
-

- Camtasia 2019 简体中文
- ¥689.00-¥689.00
-

- Luminar 3 简体中文
- ¥288.00-¥288.00
-

- Apowersoft 录屏王 简体中文
- ¥129.00-¥339.00