总结机器学习中常用的七种线性降维技术

上篇文章中我们主要总结了非线性的降维技术，本文我们来总结一下常见的线性降维技术。

1、Principal Component Analysis (PCA)

PCA是一种广泛应用的降维技术，可以将高维数据集转换为更易处理的低维表示，同时保留数据的关键特征。通过识别数据中方差最大的方向（主成分），PCA能够将数据投影到这些方向上，实现降维的目标。

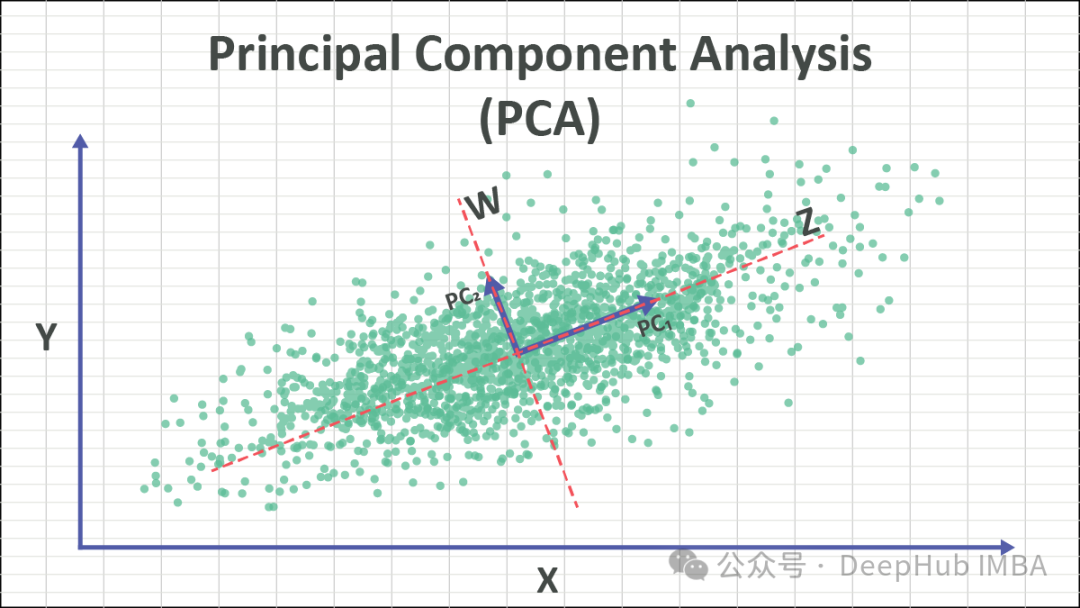
PCA的核心思想是将原始数据转换到一个新的坐标系，以最大化数据的方差。这些新坐标轴称为主成分，由原始特征线性组合而成。保留方差最大的主成分，实质上保留了数据的关键信息。通过舍弃方差较小的主成分，可以实现降维的目的。

PCA 的步骤如下：

1. 标准化数据：对原始数据进行标准化处理，使得每个特征的均值为 0，方差为 1。
2. 计算协方差矩阵：计算标准化后的数据的协方差矩阵。
3. 计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。
4. 选择主成分：按照特征值的大小选择前 k 个特征向量作为主成分，其中 k 是降维后的维度。
5. 投影数据：将原始数据投影到选定的主成分上，得到降维后的数据集。

PCA可以用于数据降维、特征提取和模式识别等任务。在使用PCA时，需要确保数据满足线性可分的基本假设，并进行必要的数据预处理和理解，以获得准确的降维效果。

2、Factor Analysis (FA)

Factor Analysis (FA) is a statistical technique used to identify the underlying structure or factors among observed variables. It aims to uncover the latent factors that account for the shared variance among the observed variables, ultimately reducing them to a smaller number of unrelated variables.

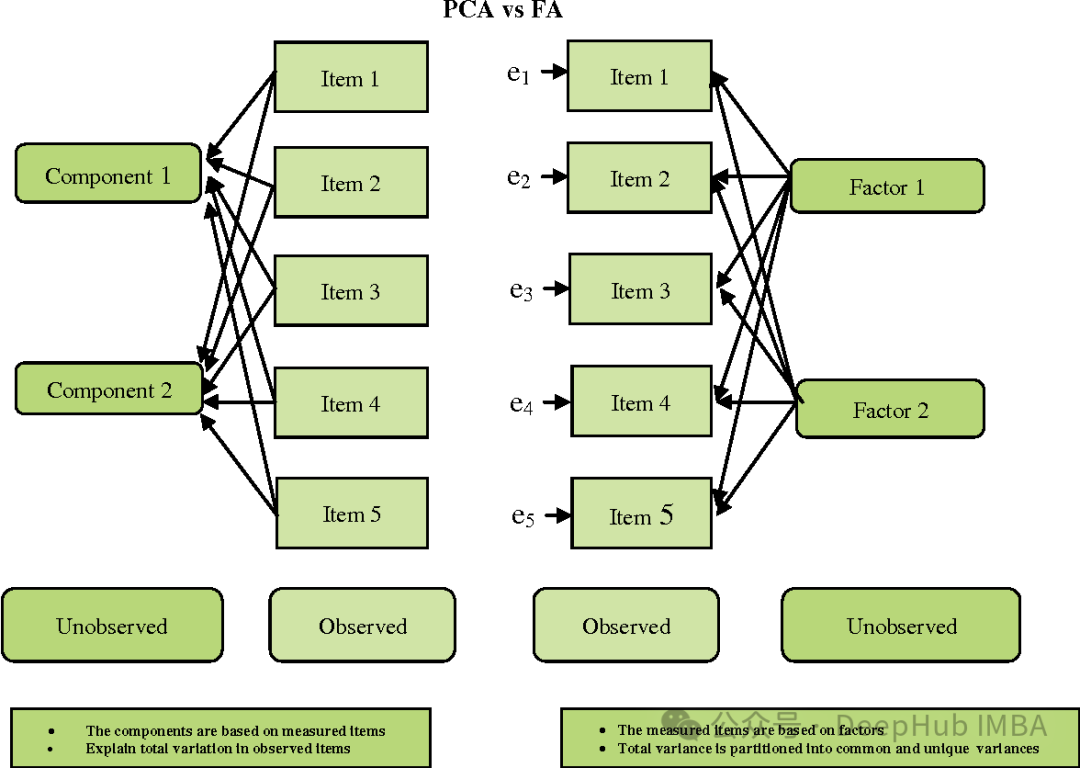
FA 和 PCA 有些相似，但也有一些重要的区别：

1. 目标：PCA 旨在找到最大方差的方向，而 FA 旨在找到潜在的变量(因素)，这些变量能够解释观察到的变量之间的共同变异。
2. 假设：PCA 假设观察到的变量是观察到的原始特征，而 FA 假设观察到的变量是潜在因素的线性组合和随机误差的总和。
3. 解释性：PCA 往往更直接，因为它的主成分是原始特征的线性组合。而 FA 的因素可能不太容易解释，因为它们是观察到的变量的线性组合，而非原始特征。
4. 旋转：在 FA 中，因素通常会进行旋转，以使它们更易于解释。

因子分析在心理学、社会科学和市场研究等领域广泛应用。它有助于简化数据集、发现潜在结构和减少测量误差。但在选择因子数量和旋转方法时需慎重，以确保结果可解释且有效。

3、Linear Discriminant Analysis，LDA

线性判别分析(Linear Discriminant Analysis，LDA)是一种用于降维和特征提取的监督学习技术。它与主成分分析(PCA)不同，因为它不仅考虑了数据的方差结构，还考虑了数据的类别信息。LDA 旨在找到一个投影方向，最大化不同类别之间的距离(类间散布)，同时最小化同一类别内部的距离(类内散布)。

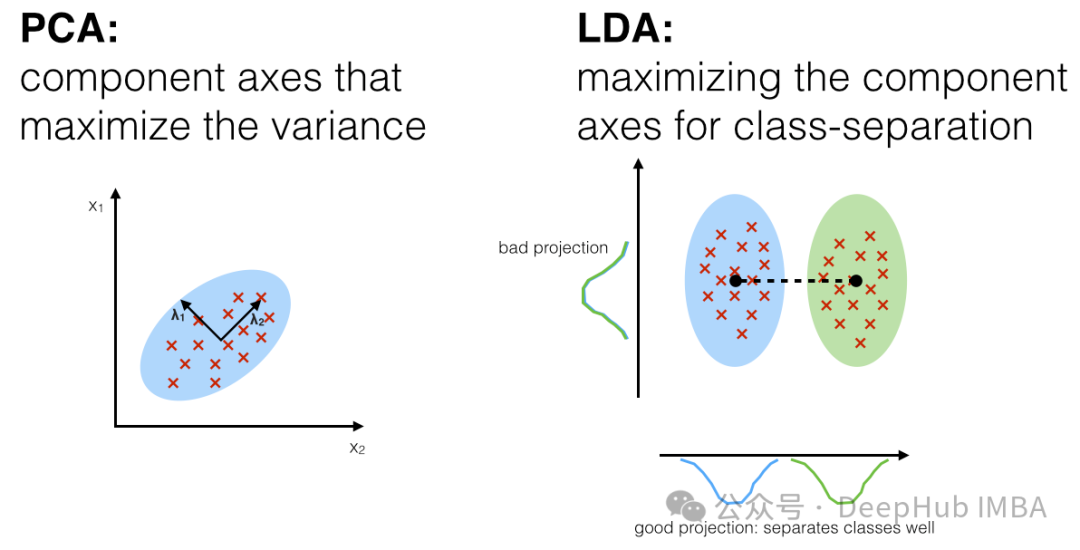
LDA 的主要步骤如下：

1. 计算类别的均值向量：对于每个类别，计算该类别下所有样本的均值向量。
2. 计算类内散布矩阵(Within-class scatter matrix)：对于每个类别，计算该类别下所有样本与其均值向量之间的散布矩阵，并将它们求和。
3. 计算类间散布矩阵(Between-class scatter matrix)：计算所有类别的均值向量与总体均值向量之间的散布矩阵。
4. 计算特征值和特征向量：对于矩阵的逆矩阵乘以类间散布矩阵，得到的矩阵进行特征值分解，得到特征值和特征向量。
5. 选择投影方向：选择特征值最大的前 k 个特征向量作为投影方向，其中 k 是降维后的维度。
6. 投影数据：将原始数据投影到选定的投影方向上，得到降维后的数据。

LDA 的优点在于它考虑了数据的类别信息，因此生成的投影能更好地区分不同类别之间的差异。它在模式识别、人脸识别、语音识别等领域中有着广泛的应用。LDA 在处理多类别和类别不平衡的情况下可能会遇到一些问题，需要特别注意。

4、Eigendecomposition

Eigendecomposition(特征值分解)是一种用于对方阵进行分解的数学技术。它将一个方阵分解为一组特征向量和特征值的乘积形式。特征向量表示了在转换中不改变方向的方向，而特征值表示了在转换中沿着这些方向的缩放比例。

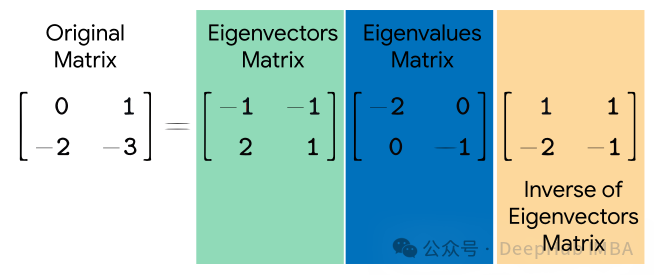
给定一个方阵 AA，其特征值分解表示为：

其中，Q是由 A 的特征向量组成的矩阵，Λ是对角矩阵，其对角线上的元素是 A的特征值。

特征值分解有许多应用，包括主成分分析(PCA)、特征脸识别、谱聚类等。在PCA中，特征值分解用于找到数据协方差矩阵的特征向量，从而找到数据的主成分。在谱聚类中，特征值分解用于找到相似性图的特征向量，从而进行聚类。特征脸识别利用了特征值分解来识别人脸图像中的重要特征。

虽然特征值分解在许多应用中非常有用，但并非所有的方阵都能进行特征值分解。例如，奇异矩阵(singular matrix)或非方阵就不能进行特征值分解。特征值分解在大型矩阵计算上可能是非常耗时的。

5、Singular value decomposition (SVD)

奇异值分解(Singular Value Decomposition，SVD)是一种用于矩阵分解的重要技术。它将一个矩阵分解为三个矩阵的乘积形式，这三个矩阵分别是一个正交矩阵、一个对角矩阵和另一个正交矩阵的转置。

给定一个 m × n 的矩阵 AA，其奇异值分解表示为：

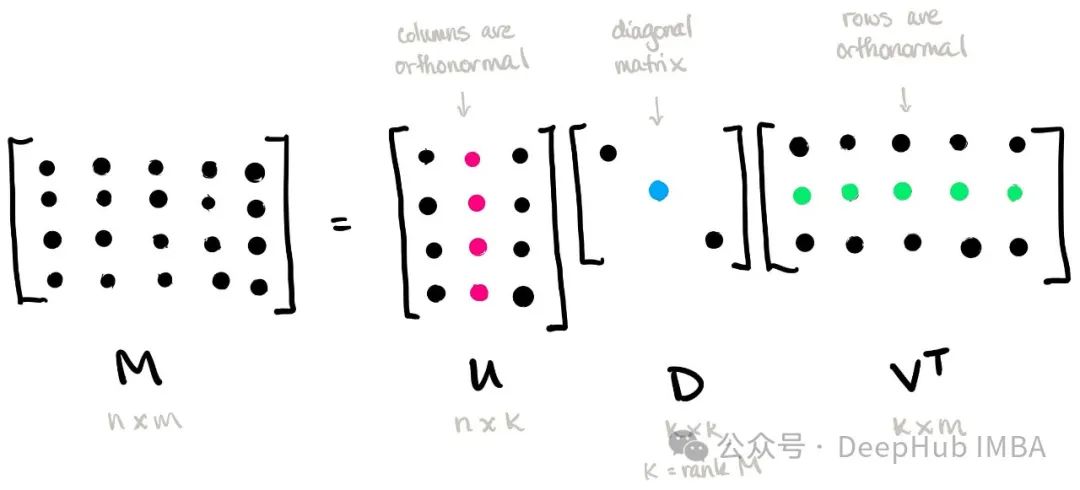
其中，U 是一个 m × m 的正交矩阵，称为左奇异向量矩阵;Σ 是一个 m × n 的对角矩阵，其对角线上的元素称为奇异值;VT 是一个 n × n 的正交矩阵的转置，称为右奇异向量矩阵。

奇异值分解具有广泛的应用，包括数据压缩、降维、矩阵逆求解、推荐系统等。在降维中，只保留奇异值较大的项，可以实现对数据的有效压缩和表示。在推荐系统中，通过奇异值分解可以对用户和项目之间的关系进行建模，从而提供个性化的推荐。

奇异值分解还可以用于矩阵逆求解，特别是对于奇异矩阵。通过保留奇异值较大的项，可以近似求解逆矩阵，从而避免了对奇异矩阵求逆的问题。

6、Truncated Singular Value Decomposition (TSVD)

截断奇异值分解(Truncated Singular Value Decomposition，TSVD)是奇异值分解(SVD)的一种变体，它在计算中只保留最重要的奇异值和对应的奇异向量，从而实现数据的降维和压缩。

给定一个 m × n 的矩阵 AA，其截断奇异值分解表示为：

其中，Uk 是一个 m × k 的正交矩阵，Σk 是一个 k × k 的对角矩阵，VkT 是一个 k × n 的正交矩阵的转置，这些矩阵对应于保留最重要的 k 个奇异值和对应的奇异向量。

TSVD 的主要优点在于它可以通过保留最重要的奇异值和奇异向量来实现数据的降维和压缩，从而减少了存储和计算成本。这在处理大规模数据集时尤其有用，因为可以显著减少所需的存储空间和计算时间。

TSVD 在许多领域都有应用，包括图像处理、信号处理、推荐系统等。在这些应用中，TSVD 可以用于降低数据的维度、去除噪声、提取关键特征等。

7、Non-Negative Matrix Factorization (NMF)

Non-Negative Matrix Factorization (NMF) 是一种用于数据分解和降维的技术，其特点是分解得到的矩阵和向量都是非负的。这使得 NMF 在许多应用中都很有用，特别是在文本挖掘、图像处理和推荐系统等领域。

给定一个非负矩阵 VV，NMF 将其分解为两个非负矩阵 WW 和 HH 的乘积形式：

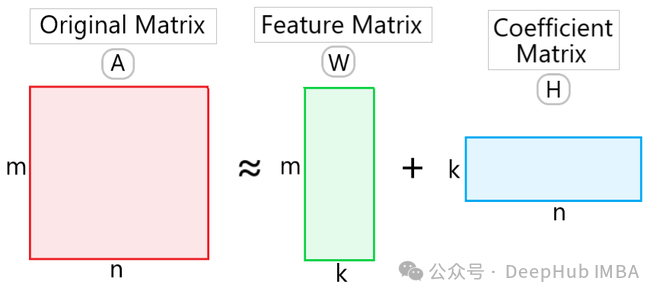
其中，W 是一个 m × k 的非负矩阵，称为基矩阵(basis matrix)或者特征矩阵(feature matrix)，H 是一个 k × n 的非负矩阵，称为系数矩阵(coefficient matrix)。这里的 k 是降维后的维度。

NMF 的优点在于它能够得到具有物理含义的分解结果，因为所有的元素都是非负的。这使得 NMF 在文本挖掘中能够发现潜在的主题，而在图像处理中能够提取出图像的特征。此外，NMF 还具有数据降维的功能，可以减少数据的维度和存储空间。

NMF 的应用包括文本主题建模、图像分割与压缩、音频信号处理、推荐系统等。在这些领域中，NMF 被广泛应用于数据分析和特征提取，以及信息检索和分类等任务中。

总结

线性降维技术是一类用于将高维数据集映射到低维空间的技术，其核心思想是通过线性变换来保留数据集的主要特征。这些线性降维技术在不同的应用场景中有其独特的优势和适用性，可以根据数据的性质和任务的要求选择合适的方法。例如，PCA适用于无监督的数据降维，而LDA适用于监督学习任务。

结合前一篇文章，我们介绍了10种非线性降维技术核7种线性降维技术，下面我们来做个总结

线性降维技术：基于线性变换将数据映射到低维空间，适用于线性可分的数据集;例如数据点分布在一个线性子空间上的情况;因为其算法简单，所以计算效率高，易于理解和实现;通常不能捕捉数据中的非线性结构，可能会导致信息丢失。

非线性降维技术：通过非线性变换将数据映射到低维空间;适用于非线性结构的数据集，例如数据点分布在流形上的情况;能够更好地保留数据中的非线性结构和局部关系，提供更好的可视化效果;计算复杂度较高，通常需要更多的计算资源和时间。

如果数据是线性可分的或者计算资源有限，可以选择线性降维技术。而如果数据包含复杂的非线性结构或者需要更好的可视化效果，可以考虑使用非线性降维技术。在实践中，也可以尝试不同的方法，并根据实际效果来选择最合适的降维技术。