北大&字节联合研究神经网络求解偏微分方程器入选Nature子刊
 发布于2024-12-07 阅读(0)
发布于2024-12-07 阅读(0)
扫一扫,手机访问
近年来,基于神经网络的偏微分方程求解器在各领域均得到了广泛关注。其中,量子变分蒙特卡洛方法(NNVMC)在量子化学领域异军突起,对于一系列问题的解决展现出超越传统方法的精确度 [1, 2, 3, 4]。北京大学与字节跳动研究部门 ByteDance Research 联合开发的计算框架 Forward Laplacian 创新地利用 Laplace 算子前向传播计算,为 NNVMC 领域提供了十倍的加速,从而大幅降低计算成本,达成该领域多项 State of the Art,同时也助力该领域向更多的科学难题发起冲击。该工作以《A computational framework for neural network-based variational Monte Carlo with Forward Laplacian》为题的论文已发表于国际顶级期刊《Nature Machine Intelligence》,相关代码已开源。

- 论文链接:https://www.nature.com/articles/s42256-024-00794-x
- 代码地址:
- https://github.com/bytedance/LapNet。
- https://github.com/YWolfeee/lapjax。
这项工作一经提出便引起了相关研究人员的高度关注,已经有多个开源项目围绕着这项工作展开,编程框架 JAX 也打算将其纳入计划中。
这项工作是由北京大学智能学院王立威课题组和物理学院陈基课题组与字节跳动研究部门共同合作完成的。在这个项目中,多位北京大学博士生在字节跳动研究部门实习,为研究和开发工作提供了宝贵的支持。
背景简介
基于神经网络的量子变分蒙特卡洛方法(NNVMC)已经成为量子化学 - 从头计算领域中备受关注的技术。NNVMC具有高度的精度和适用范围广的优势。然而,其计算成本较高是其主要挑战之一,这也限制了该方法在实际化学问题中的应用。
提出了一套名为 "Forward Laplacian" 的全新计算框架,通过利用 Laplace 算子进行前向传播,大幅提高了 NNVMC 方法的计算效率。这一创新为人工智能在微观量子问题领域的应用带来了新的可能性。
方法介绍
Forward Laplacian 框架
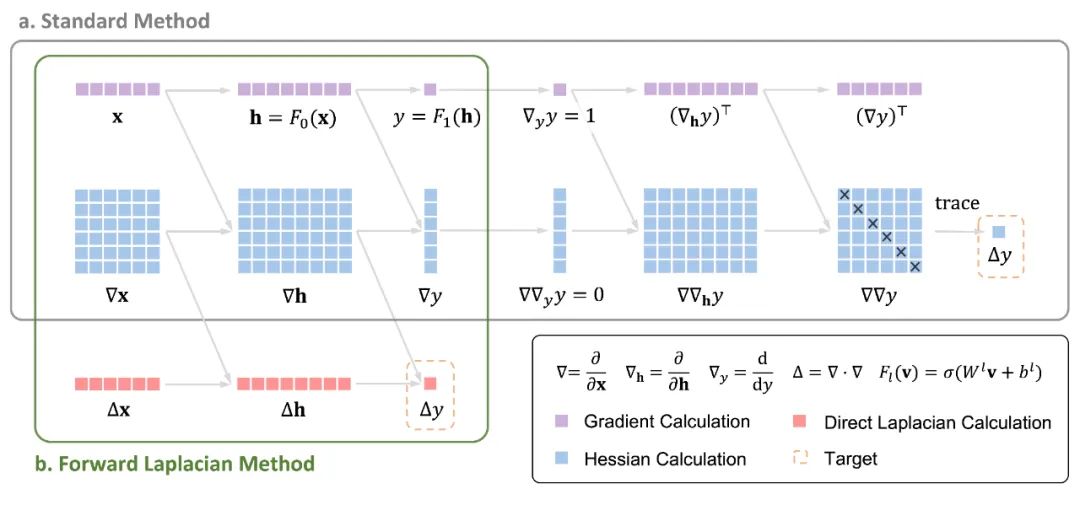
在 NNVMC 方法中,神经网络的目标函数是微观体系的能量,包括动能与势能两项。其中动能项涉及对神经网络的拉普拉斯算子的计算,这也是 NNVMC 中耗时最长的计算瓶颈。现有的自动微分框架在计算拉普拉斯算子时,需要先计算黑塞矩阵,再求得拉普拉斯项(即黑塞矩阵的迹)。而作者所提出的计算框架 "Forward Laplacian" 则通过一次前向传播直接求得拉普拉斯项,避免了黑塞矩阵的计算,从而削减了整体计算的规模,实现了显著加速。
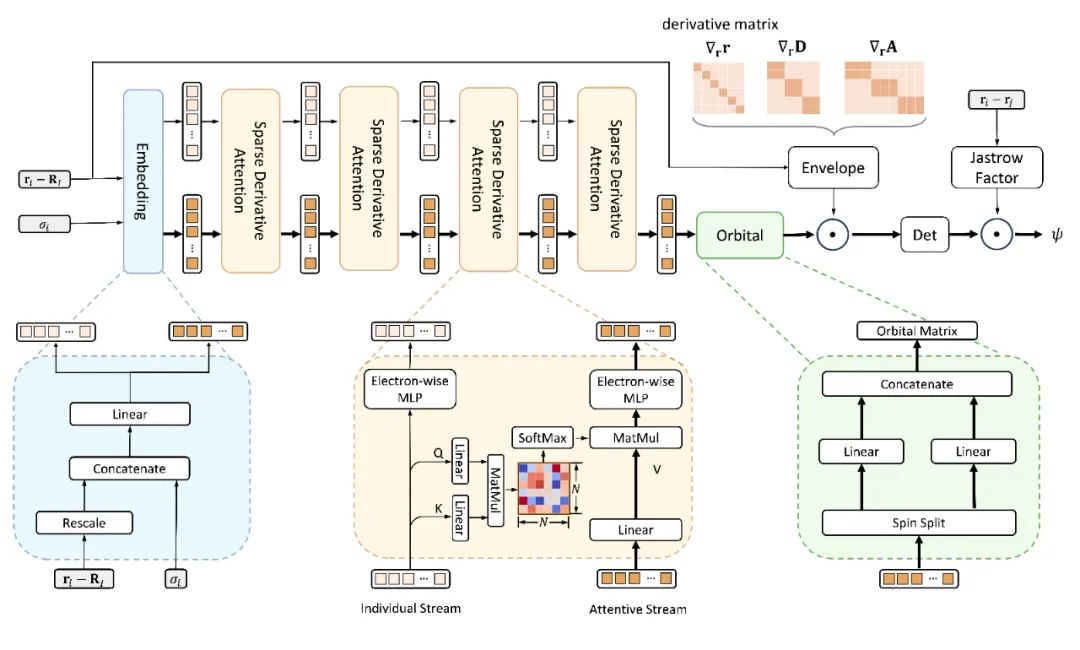
LapNet 网络
Forward Laplacian 框架的另一个显著特点是其能够有效利用神经网络梯度计算中的稀疏性。为了进一步提高网络的计算效率,提出了一种名为 LapNet 的神经网络结构。通过增加网络中的稀疏性,LapNet 在不影响精度的情况下,极大地提升了计算效率。
计算结果
绝对能量
作者首先就方法的效率及精度同当前 NNVMC 领域有代表性的几项工作进行了比较。从绝对能量的计算结果而言,作者提出的 LapNet 在 Forward Laplacian 框架下的效率高于参考工作数倍,精度上也与 SOTA 保持一致。此外,如果在相同计算资源(即相同 GPU hour)的情况下比较,LapNet 的计算结果可以显著优于之前的 SOTA。
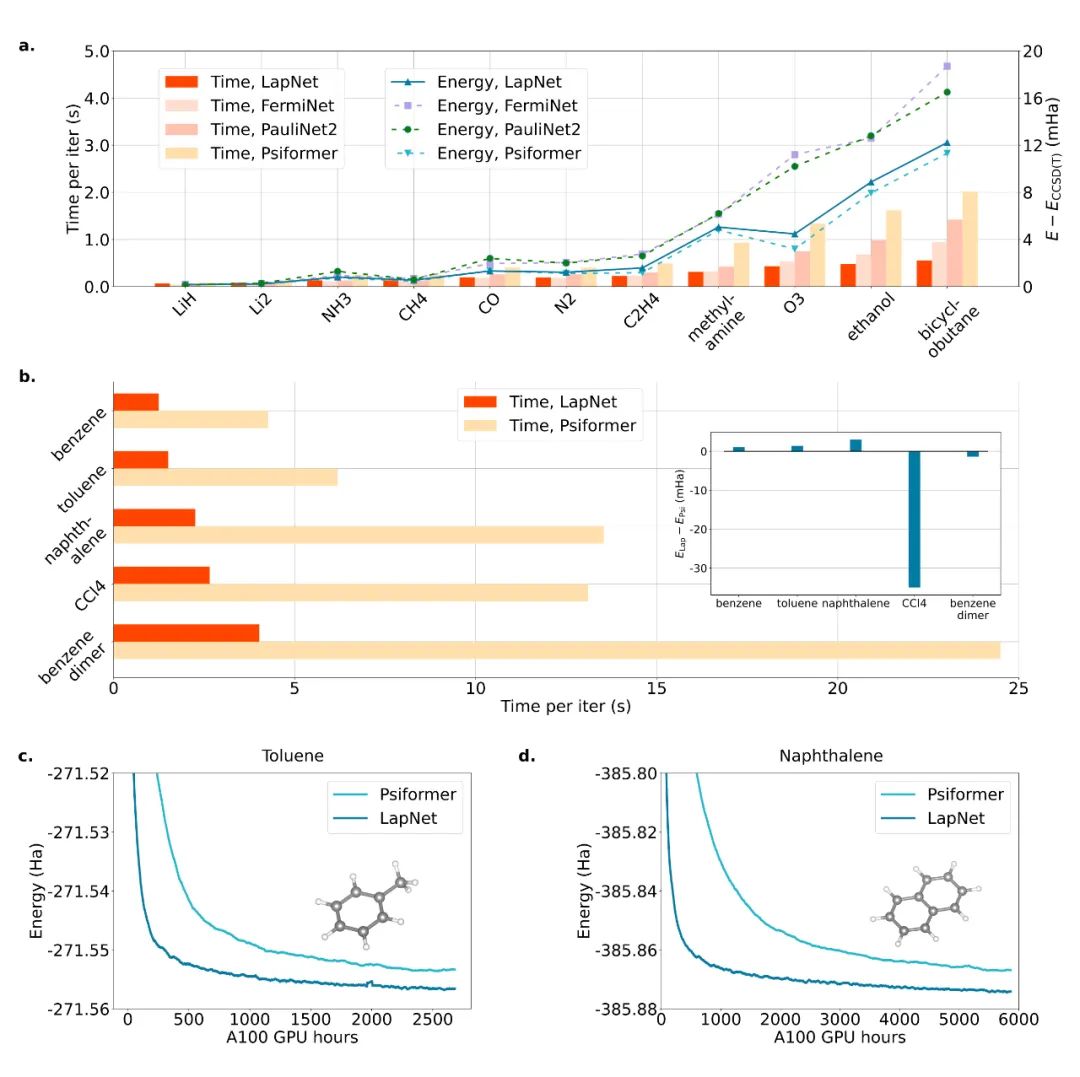
加速标度
为了更明确地研究作者所提出方法相比于之前 SOTA 的加速标度,作者在不同大小的链式聚乙烯体系上进行了测试,结果可以很明显地看到 Forward Laplacian 工作带来的 O (n) 加速。此处 n 为目标分子中的电子数目。
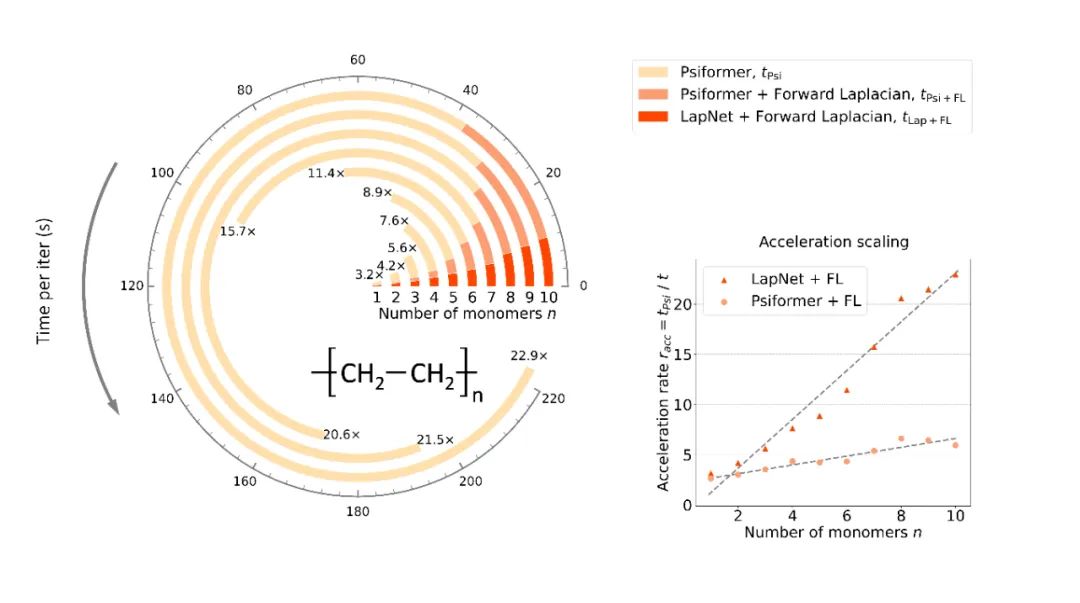
相对能量
在物理、化学研究中,相对能量相较于绝对能量具有更明确的物理意义。作者也在一系列的体系上进行了测试,均取得了理想结果。
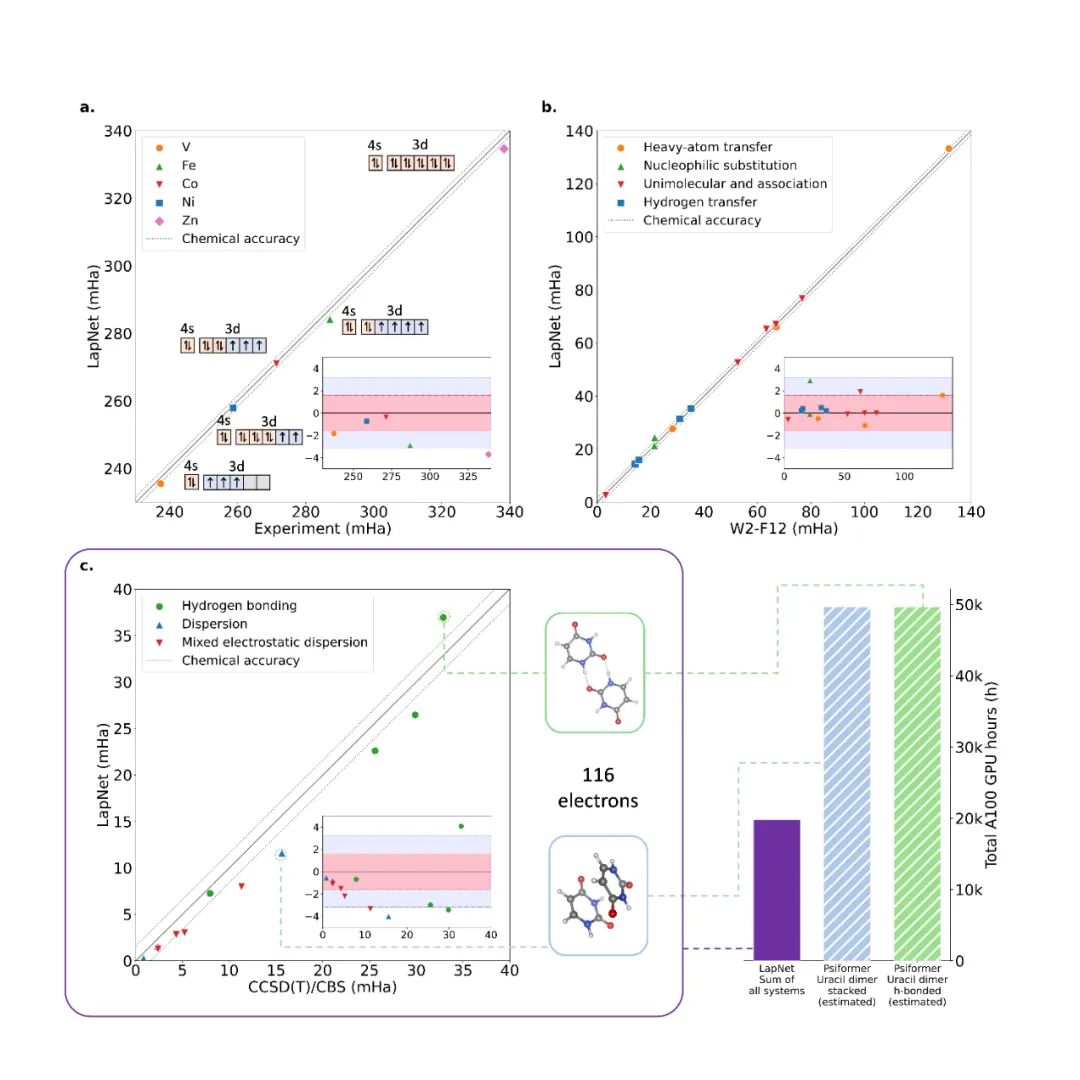
总结
为降低基于神经网络的量子变分蒙特卡洛方法(NNVMC)的使用门槛,北京大学与字节跳动研究部门 ByteDance Research 联合开发了计算框架 Forward Laplacian,实现了十倍的加速。该工作已受到相关研究人员的广泛关注,期望能够推动 NNVMC 方法在更多科学问题中发挥重要作用。
参考文献
[1] Han, J., Zhang, L., & Weinan, E. (2019). Solving many-electron Schrödinger equation using deep neural networks. Journal of Computational Physics, 399, 108929.
[2] Hermann, J., Schätzle, Z., & Noé, F. (2020). Deep-neural-network solution of the electronic Schrödinger equation. Nature Chemistry, 12 (10), 891-897.
[3] Pfau, D., Spencer, J. S., Matthews, A. G., & Foulkes, W. M. C. (2020). Ab initio solution of the many-electron Schrödinger equation with deep neural networks. Physical Review Research, 2 (3), 033429.
[4] Li, X., Li, Z., & Chen, J. (2022). Ab initio calculation of real solids via neural network ansatz. Nature Communications, 13 (1), 7895.
下一篇:免费在线工具:简单创建PHP文件
产品推荐
-

售后无忧
立即购买>- DAEMON Tools Lite 10【序列号终身授权 + 中文版 + Win】
-
¥150.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Ultra 5【序列号终身授权 + 中文版 + Win】
-
¥198.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Pro 8【序列号终身授权 + 中文版 + Win】
-
¥189.00
office旗舰店
-

售后无忧
立即购买>- CorelDRAW X8 简体中文【标准版 + Win】
-
¥1788.00
office旗舰店
-
 正版软件
正版软件
- 区块链最大交易平台
- 币安是加密货币交易量最大的平台。其优势包括广泛的加密货币选择、低交易费用、高级交易功能、强大的安全措施和用户友好界面。
- 4分钟前 0
-
 正版软件
正版软件
- mexc提币记录能保存多久
- 在MEXC交易所,提币记录会永久保存,用户可以随时查看和下载他们的提币历史记录,对于核对交易、安全审计、纳税申报和追踪资金至关重要。用户可以通过登录账户、选择“资产”和“充提币”,然后在“提币”标签下导出记录来查看和下载提币记录。虽然记录永久保存,但用户应定期备份,以确保意外情况下的访问。
- 9分钟前 0
-
 正版软件
正版软件
- 手机购买狗狗币教程
- 要在手机上购买狗狗币,可以通过加密货币交易所,步骤为:选择交易所,下载并注册;验证身份以符合法规;为账户充值;在交易界面搜索“狗狗币”;输入购买数量和价格,选择“买入”或“市价买入”;检查订单详情并确认交易;狗狗币将存储在交易所的数字钱包中,可选择留在交易所或转移到个人钱包。如何通过手机购买狗狗币步骤1:选择加密货币交易所在手机上下载并注册一个信誉良好的加密货币交易所,例如Coinbase、Binance或Kraken。步骤2:验证身份为了遵守法规,大多数交易所需要您验证身份。这通常需要您提供个人信息,例
- 24分钟前 0
-
 正版软件
正版软件
- 币圈知名交易所
- 币圈知名交易所有哪些?国内交易所:火币网:中国早期成立的加密货币交易所,交易量庞大,支持多种交易对。币安中国:币安旗下的中国子公司,提供合规的加密货币交易服务。OKX:全球著名的加密货币交易所,提供丰富的交易产品和服务。中币网:中国老牌加密货币交易所,以币币交易和法币交易为主。抹茶网:主要面向亚洲市场的加密货币交易所,交易费用较低。国外交易所:币安:全球最大的加密货币交易所,提供超百种加密货币的交易服务。Coinbase:美国合规的加密货币交易所,面向个人和机构投资者。Kraken:全球知名的老牌交易所,
- 39分钟前 0
-
 正版软件
正版软件
- 加密货币排名前十名
- 截至2023年3月,加密货币排名前十名包括:比特币、以太坊、泰达币、币安币、瑞波币、卡尔达诺、狗狗币、波卡币、索拉纳和Polygon,市值总额约为1.2万亿美元;加密货币用途广泛,包括价值存储、支付、智能合约和DeFi;市场波动性大,监管仍在进行中,其未来不确定。
- 54分钟前 0