商城首页欢迎来到中国正版软件门户
文章教程　|　产品大全　|　软件问答

您的位置：首页 > 业界资讯 >顶级深度学习算法大揭秘！

顶级深度学习算法大揭秘！

　　发布于2024-12-16　阅读（0）

扫一扫，手机访问

自2006年深度学习概念被提出以来，20年快过去了，深度学习作为人工智能领域的一场革命，已经催生了许多具有影响力的算法。那么，你所认为深度学习的top10算法有哪些呢？

超强！深度学习Top10算法！

以下是我心目中深度学习的顶尖算法，它们在创新性、应用价值和影响力方面都占据重要地位。

1、深度神经网络（DNN）

背景：深度神经网络（DNN）也叫多层感知机，是最普遍的深度学习算法，发明之初由于算力瓶颈而饱受质疑，直到近些年算力、数据的爆发才迎来突破。

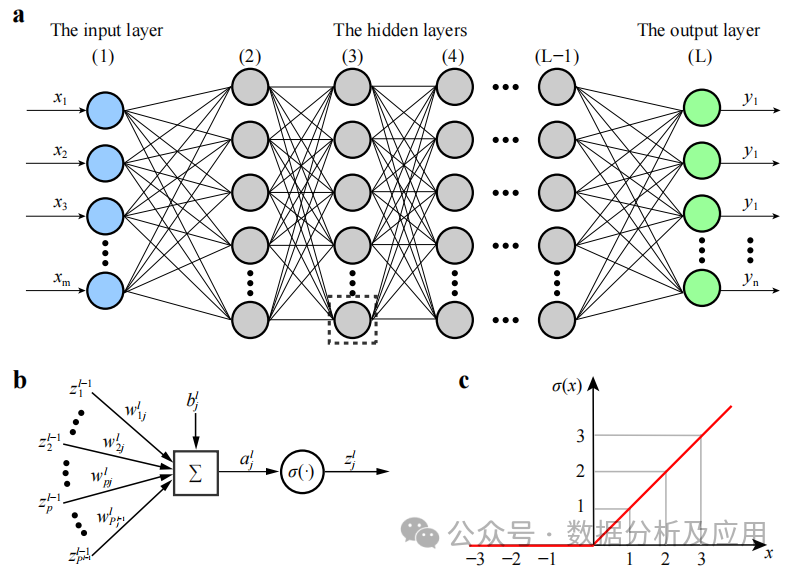
超强！深度学习Top10算法！

DNN是一种神经网络模型，它包含多个隐藏层。在该模型中，每一层将输入传递给下一层，并利用非线性激活函数引入学习的非线性特性。通过叠加这些非线性变换，DNN可以学习输入数据的复杂特征表示。

模型训练涉及使用反向传播算法和梯度下降优化算法来不断调整权重。在训练中，通过计算损失函数对权重的梯度，然后利用梯度下降或其他优化算法来更新权重，以使损失函数最小化。

优点：能够学习输入数据的复杂特征，并捕获非线性关系。具有强大的特征学习和表示能力。

网络深度增加会导致梯度消失问题加剧，训练不稳定。此外，模型容易陷入局部最小值，需要复杂的初始化策略和正则化技术。

使用场景：图像分类、语音识别、自然语言处理、推荐系统等。

Python示例代码：

import numpy as npfrom keras.models import Sequentialfrom keras.layers import Dense# 假设有10个输入特征和3个输出类别input_dim = 10num_classes = 3# 创建DNN模型model = Sequential()model.add(Dense(64, activatinotallow='relu', input_shape=(input_dim,)))model.add(Dense(32, activatinotallow='relu'))model.add(Dense(num_classes, activatinotallow='softmax'))# 编译模型，选择优化器和损失函数model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])# 假设有100个样本的训练数据和标签X_train = np.random.rand(100, input_dim)y_train = np.random.randint(0, 2, size=(100, num_classes))# 训练模型model.fit(X_train, y_train, epochs=10)

2、卷积神经网络（CNN）

模型原理：卷积神经网络（CNN）是一种专门为处理图像数据而设计的神经网络，由Lechun大佬设计的Lenet是CNN的开山之作。CNN通过使用卷积层来捕获局部特征，并通过池化层来降低数据的维度。卷积层对输入数据进行局部卷积操作，并使用参数共享机制来减少模型的参数数量。池化层则对卷积层的输出进行下采样，以降低数据的维度和计算复杂度。这种结构特别适合处理图像数据。

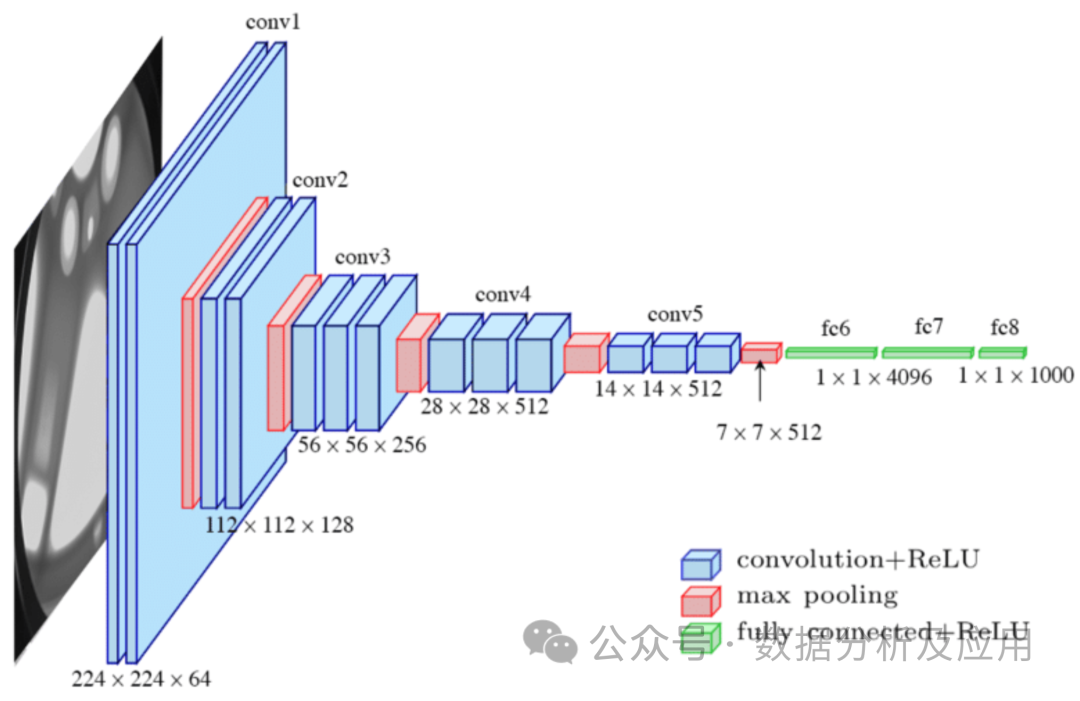
超强！深度学习Top10算法！

模型训练涉及使用反向传播算法和梯度下降优化算法来不断调整权重。在训练中，通过计算损失函数对权重的梯度，然后利用梯度下降或其他优化算法来更新权重，以使损失函数最小化。

优点：能够有效地处理图像数据，并捕获局部特征。具有较少的参数数量，降低了过拟合的风险。

缺点：对于序列数据或长距离依赖关系可能不太适用。可能需要对输入数据进行复杂的预处理。

使用场景：图像分类、目标检测、语义分割等。

Python示例代码

from keras.models import Sequentialfrom keras.layers import Conv2D, MaxPooling2D, Flatten, Dense# 假设输入图像的形状是64x64像素，有3个颜色通道input_shape = (64, 64, 3)# 创建CNN模型model = Sequential()model.add(Conv2D(32, (3, 3), activatinotallow='relu', input_shape=input_shape))model.add(MaxPooling2D((2, 2)))model.add(Conv2D(64, (3, 3), activatinotallow='relu'))model.add(Flatten())model.add(Dense(128, activatinotallow='relu'))model.add(Dense(num_classes, activatinotallow='softmax'))# 编译模型，选择优化器和损失函数model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])# 假设有100个样本的训练数据和标签X_train = np.random.rand(100, *input_shape)y_train = np.random.randint(0, 2, size=(100, num_classes))# 训练模型model.fit(X_train, y_train, epochs=10)

3、残差网络（ResNet）

随着深度学习的快速发展，深度神经网络在多个领域取得了显著的成功。然而，深度神经网络的训练面临着梯度消失和模型退化等问题，这限制了网络的深度和性能。为了解决这些问题，残差网络（ResNet）被提出。

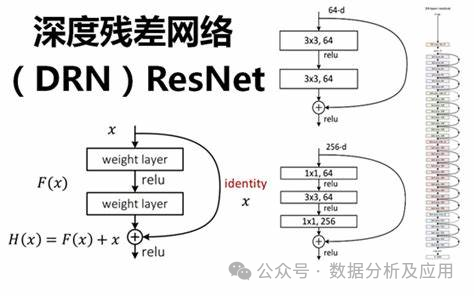
超强！深度学习Top10算法！

模型原理：

ResNet通过引入“残差块”来解决深度神经网络中的梯度消失和模型退化问题。残差块由一个“跳跃连接”和一个或多个非线性层组成，使得梯度可以直接从后面的层反向传播到前面的层，从而更好地训练深度神经网络。通过这种方式，ResNet能够构建非常深的网络结构，并在多个任务上取得了优异的性能。

模型训练：

ResNet的训练通常使用反向传播算法和优化算法（如随机梯度下降）。在训练过程中，通过计算损失函数关于权重的梯度，并使用优化算法更新权重，以最小化损失函数。此外，为了加速训练过程和提高模型的泛化能力，还可以采用正则化技术、集成学习等方法。

优点：

  1. 解决了梯度消失和模型退化问题：通过引入残差块和跳跃连接，ResNet能够更好地训练深度神经网络，避免了梯度消失和模型退化的问题。
  2. 构建了非常深的网络结构：由于解决了梯度消失和模型退化问题，ResNet能够构建非常深的网络结构，从而提高了模型的性能。
  3. 在多个任务上取得了优异的性能：由于其强大的特征学习和表示能力，ResNet在多个任务上取得了优异的性能，如图像分类、目标检测等。

缺点：

  1. 计算量大：由于ResNet通常构建非常深的网络结构，因此计算量较大，需要较高的计算资源和时间进行训练。
  2. 参数调优难度大：ResNet的参数数量众多，需要花费大量时间和精力进行调优和超参数选择。
  3. 对初始化权重敏感：ResNet对初始化权重的选择敏感度高，如果初始化权重不合适，可能会导致训练不稳定或过拟合问题。

使用场景：

ResNet在计算机视觉领域有着广泛的应用场景，如图像分类、目标检测、人脸识别等。此外，ResNet还可以用于自然语言处理、语音识别等领域。

Python示例代码（简化版）：

在这个简化版的示例中，我们将演示如何使用Keras库构建一个简单的ResNet模型。

from keras.models import Sequentialfrom keras.layers import Conv2D, Add, Activation, BatchNormalization, Shortcutdef residual_block(input, filters):x = Conv2D(filters=filters, kernel_size=(3, 3), padding='same')(input)x = BatchNormalization()(x)x = Activation('relu')(x)x = Conv2D(filters=filters, kernel_size=(3, 3), padding='same')(x)x = BatchNormalization()(x)x = Activation('relu')(x)return x

4、LSTM（长短时记忆网络）

在处理序列数据时，传统的循环神经网络（RNN）面临着梯度消失和模型退化等问题，这限制了网络的深度和性能。为了解决这些问题，LSTM被提出。

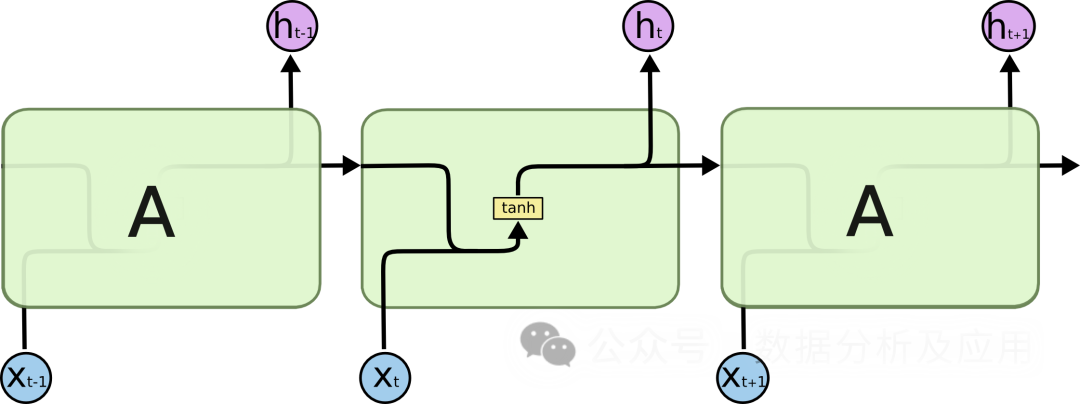
超强！深度学习Top10算法！

模型原理：

LSTM通过引入“门控”机制来控制信息的流动，从而解决梯度消失和模型退化问题。LSTM有三个门控机制：输入门、遗忘门和输出门。输入门决定了新信息的进入，遗忘门决定了旧信息的遗忘，输出门决定最终输出的信息。通过这些门控机制，LSTM能够在长期依赖问题上表现得更好。

模型训练：

LSTM的训练通常使用反向传播算法和优化算法（如随机梯度下降）。在训练过程中，通过计算损失函数关于权重的梯度，并使用优化算法更新权重，以最小化损失函数。此外，为了加速训练过程和提高模型的泛化能力，还可以采用正则化技术、集成学习等方法。

优点：

  1. 解决梯度消失和模型退化问题：通过引入门控机制，LSTM能够更好地处理长期依赖问题，避免了梯度消失和模型退化的问题。
  2. 构建非常深的网络结构：由于解决了梯度消失和模型退化问题，LSTM能够构建非常深的网络结构，从而提高了模型的性能。
  3. 在多个任务上取得了优异的性能：由于其强大的特征学习和表示能力，LSTM在多个任务上取得了优异的性能，如文本生成、语音识别、机器翻译等。

缺点：

  1. 参数调优难度大：LSTM的参数数量众多，需要花费大量时间和精力进行调优和超参数选择。
  2. 对初始化权重敏感：LSTM对初始化权重的选择敏感度高，如果初始化权重不合适，可能会导致训练不稳定或过拟合问题。
  3. 计算量大：由于LSTM通常构建非常深的网络结构，因此计算量较大，需要较高的计算资源和时间进行训练。

使用场景：

LSTM在自然语言处理领域有着广泛的应用场景，如文本生成、机器翻译、语音识别等。此外，LSTM还可以用于时间序列分析、推荐系统等领域。

Python示例代码（简化版）：

from keras.models import Sequentialfrom keras.layers import LSTM, Densedef lstm_model(input_shape, num_classes):model = Sequential()model.add(LSTM(units=128, input_shape=input_shape))# 添加一个LSTM层model.add(Dense(units=num_classes, activatinotallow='softmax'))# 添加一个全连接层return model

5、Word2Vec

Word2Vec模型是表征学习的开山之作。由Google的科学家们开发的一种用于自然语言处理的(浅层)神经网络模型。Word2Vec模型的目标是将每个词向量化为一个固定大小的向量，这样相似的词就可以被映射到相近的向量空间中。

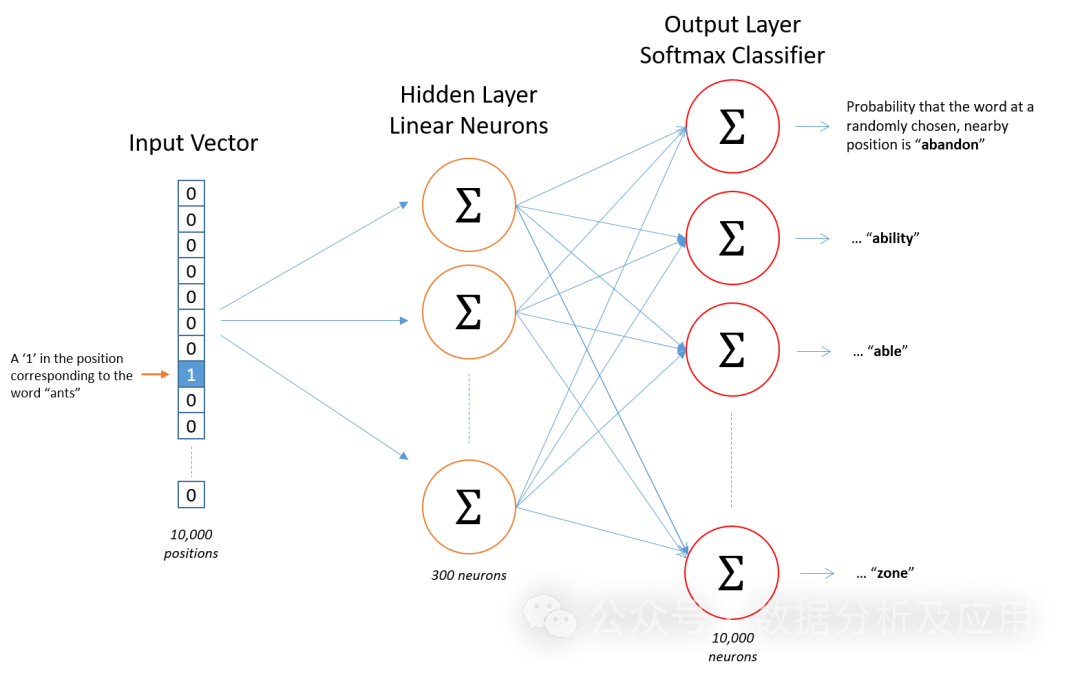
超强！深度学习Top10算法！

模型原理

Word2Vec模型基于神经网络，利用输入的词预测其上下文词。在训练过程中，模型尝试学习到每个词的向量表示，使得在给定上下文中出现的词与目标词的向量表示尽可能接近。这种训练方式称为“Skip-gram”或“Continuous Bag of Words”（CBOW）。

模型训练

训练Word2Vec模型需要大量的文本数据。首先，将文本数据预处理为一系列的词或n-gram。然后，使用神经网络训练这些词或n-gram的上下文。在训练过程中，模型会不断地调整词的向量表示，以最小化预测误差。

优点

  1. 语义相似性: Word2Vec能够学习到词与词之间的语义关系，相似的词在向量空间中距离相近。
  2. 高效的训练: Word2Vec的训练过程相对高效，可以在大规模文本数据上训练。
  3. 可解释性: Word2Vec的词向量具有一定的可解释性，可以用于诸如聚类、分类、语义相似性计算等任务。

缺点

  1. 数据稀疏性: 对于大量未在训练数据中出现的词，Word2Vec可能无法为其生成准确的向量表示。
  2. 上下文窗口: Word2Vec只考虑了固定大小的上下文，可能会忽略更远的依赖关系。
  3. 计算复杂度: Word2Vec的训练和推理过程需要大量的计算资源。
  4. 参数调整: Word2Vec的性能高度依赖于超参数（如向量维度、窗口大小、学习率等）的设置。

使用场景

Word2Vec被广泛应用于各种自然语言处理任务，如文本分类、情感分析、信息提取等。例如，可以使用Word2Vec来识别新闻报道的情感倾向（正面或负面），或者从大量文本中提取关键实体或概念。

Python示例代码

from gensim.models import Word2Vecfrom nltk.tokenize import word_tokenizefrom nltk.corpus import abcimport nltk# 下载和加载abc语料库nltk.download('abc')corpus = abc.sents()# 将语料库分词并转换为小写sentences = [[word.lower() for word in word_tokenize(text)] for text in corpus]# 训练Word2Vec模型model = Word2Vec(sentences, vector_size=100, window=5, min_count=5, workers=4)# 查找词"the"的向量表示vector = model.wv['the']# 计算与其他词的相似度similarity = model.wv.similarity('the', 'of')# 打印相似度值print(similarity)

6、Transformer

背景：

在深度学习的早期阶段，卷积神经网络（CNN）在图像识别和自然语言处理领域取得了显著的成功。然而，随着任务复杂度的增加，序列到序列（Seq2Seq）模型和循环神经网络（RNN）成为处理序列数据的常用方法。尽管RNN及其变体在某些任务上表现良好，但它们在处理长序列时容易遇到梯度消失和模型退化问题。为了解决这些问题，Transformer模型被提出。而后的GPT、Bert等大模型都是基于Transformer实现了卓越的性能！

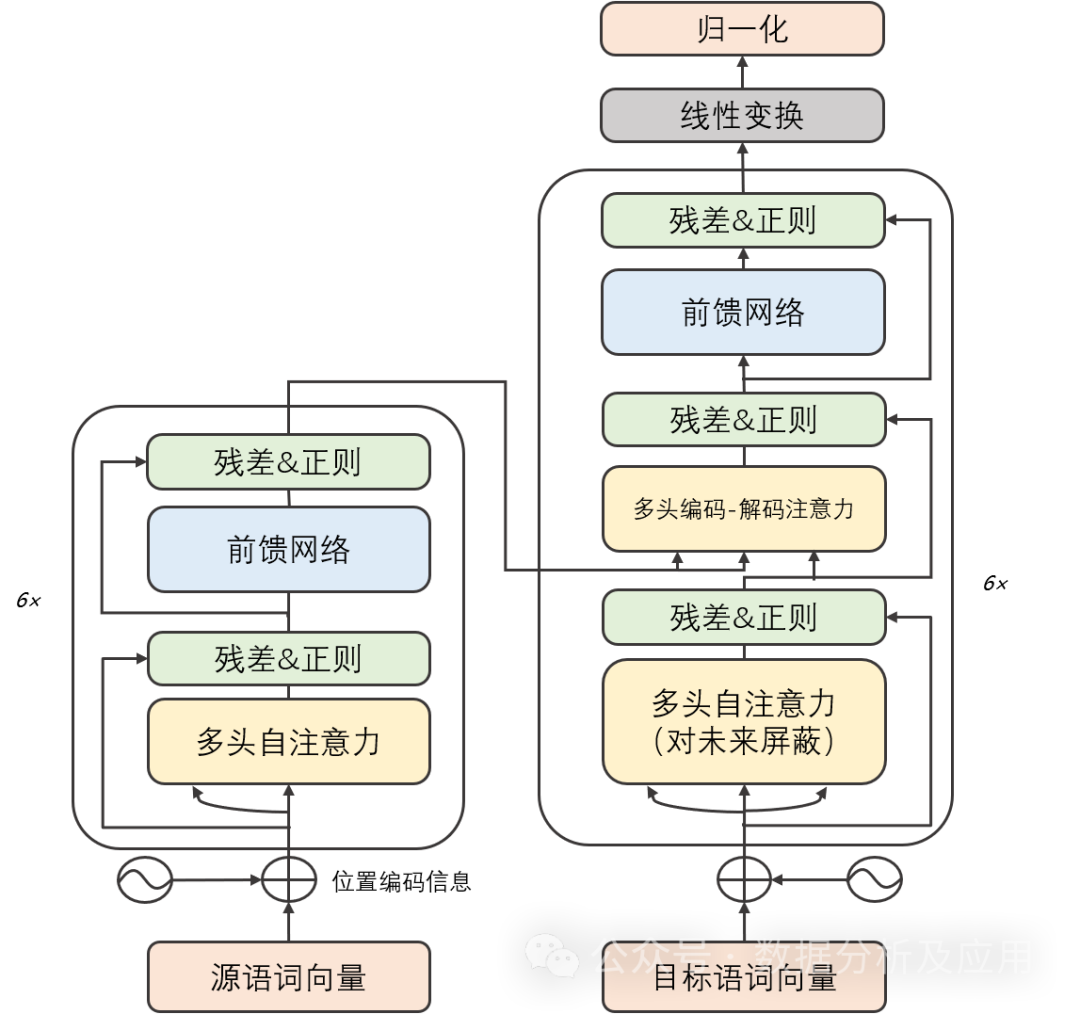
超强！深度学习Top10算法！

模型原理：

Transformer模型主要由两部分组成：编码器和解码器。每个部分都由多个相同的“层”组成。每一层包含两个子层：自注意力子层和线性前馈神经网络子层。自注意力子层利用点积注意力机制计算输入序列中每个位置的表示，而线性前馈神经网络子层则将自注意力层的输出作为输入，并产生一个输出表示。此外，编码器和解码器都包含一个位置编码层，用于捕获输入序列中的位置信息。

模型训练：

Transformer模型的训练通常使用反向传播算法和优化算法（如随机梯度下降）。在训练过程中，通过计算损失函数关于权重的梯度，并使用优化算法更新权重，以最小化损失函数。此外，为了加速训练过程和提高模型的泛化能力，还可以采用正则化技术、集成学习等方法。

优点：

  1. 解决了梯度消失和模型退化问题：由于Transformer模型采用自注意力机制，它能够更好地捕捉序列中的长期依赖关系，从而避免了梯度消失和模型退化的问题。
  2. 高效的并行计算能力：由于Transformer模型的计算是可并行的，因此在GPU上可以快速地进行训练和推断。
  3. 在多个任务上取得了优异的性能：由于其强大的特征学习和表示能力，Transformer模型在多个任务上取得了优异的性能，如机器翻译、文本分类、语音识别等。

缺点：

  1. 计算量大：由于Transformer模型的计算是可并行的，因此需要大量的计算资源进行训练和推断。
  2. 对初始化权重敏感：Transformer模型对初始化权重的选择敏感度高，如果初始化权重不合适，可能会导致训练不稳定或过拟合问题。
  3. 无法学习长期依赖关系：尽管Transformer模型解决了梯度消失和模型退化问题，但在处理非常长的序列时仍然存在挑战。

使用场景：

Transformer模型在自然语言处理领域有着广泛的应用场景，如机器翻译、文本分类、文本生成等。此外，Transformer模型还可以用于图像识别、语音识别等领域。

Python示例代码（简化版）：

import torchimport torch.nn as nnimport torch.nn.functional as Fclass TransformerModel(nn.Module):def __init__(self, vocab_size, embedding_dim, num_heads, num_layers, dropout_rate=0.5):super(TransformerModel, self).__init__()self.embedding = nn.Embedding(vocab_size, embedding_dim)self.transformer = nn.Transformer(d_model=embedding_dim, nhead=num_heads, num_encoder_layers=num_layers, num_decoder_layers=num_layers, dropout=dropout_rate)self.fc = nn.Linear(embedding_dim, vocab_size)def forward(self, src, tgt):embedded = self.embedding(src)output = self.transformer(embedded)output = self.fc(output)return output pip install transformers

7、生成对抗网络（GAN）

GAN的思想源于博弈论中的零和游戏，其中一个玩家试图生成最逼真的假数据，而另一个玩家则尝试区分真实数据与假数据。GAN由蒙提霍尔问题（一种生成模型与判别模型组合的问题）演变而来，但与蒙提霍尔问题不同，GAN不强调逼近某些概率分布或生成某种样本，而是直接使用生成模型与判别模型进行对抗。

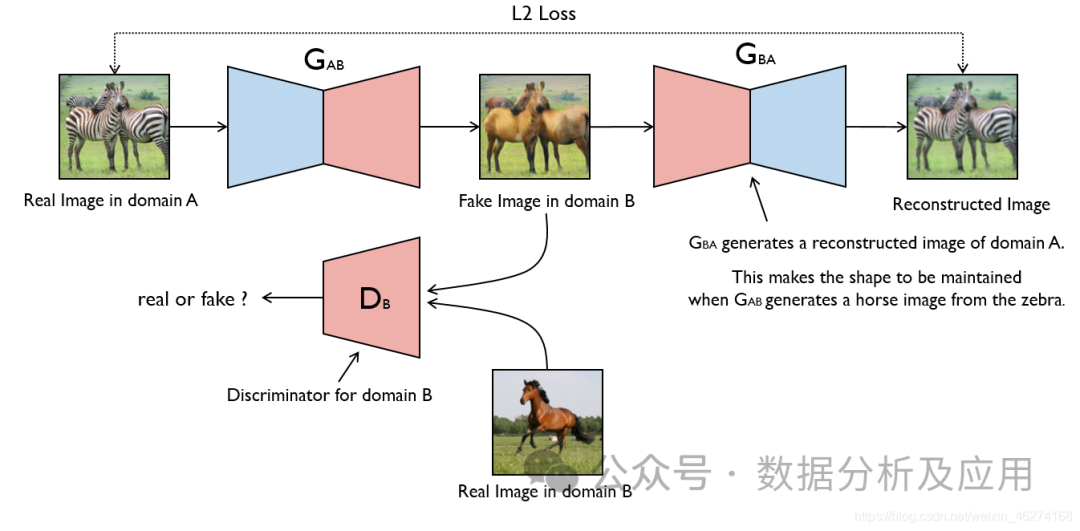
超强！深度学习Top10算法！

模型原理：

GAN由两部分组成：生成器（Generator）和判别器（Discriminator）。生成器的任务是生成假数据，而判别器的任务是判断输入的数据是来自真实数据集还是生成器生成的假数据。在训练过程中，生成器和判别器进行对抗，不断调整参数，直到达到一个平衡状态。此时，生成器生成的假数据足够逼真，使得判别器无法区分真实数据与假数据。

模型训练：

GAN的训练过程是一个优化问题。在每个训练步骤中，首先使用当前参数下的生成器生成假数据，然后使用判别器判断这些数据是真实的还是生成的。接着，根据这个判断结果更新判别器的参数。同时，为了防止判别器过拟合，还需要对生成器进行训练，使得生成的假数据能够欺骗判别器。这个过程反复进行，直到达到平衡状态。

优点：

  1. 强大的生成能力：GAN能够学习到数据的内在结构和分布，从而生成非常逼真的假数据。
  2. 无需显式监督：GAN的训练过程中不需要显式的标签信息，只需要真实数据即可。
  3. 灵活性高：GAN可以与其他模型结合使用，例如与自编码器结合形成AutoGAN，或者与卷积神经网络结合形成DCGAN等。

缺点：

  1. 训练不稳定：GAN的训练过程不稳定，容易陷入模式崩溃（mode collapse）的问题，即生成器只生成某一种样本，导致判别器无法正确判断。
  2. 难以调试：GAN的调试比较困难，因为生成器和判别器之间存在复杂的相互作用。
  3. 难以评估：由于GAN的生成能力很强，很难评估其生成的假数据的真实性和多样性。

使用场景：

  1. 图像生成：GAN最常用于图像生成任务，可以生成各种风格的图像，例如根据文字描述生成图像、将一幅图像转换为另一风格等。
  2. 数据增强：GAN可以用于生成类似真实数据的假数据，用于扩充数据集或改进模型的泛化能力。
  3. 图像修复：GAN可以用于修复图像中的缺陷或去除图像中的噪声。
  4. 视频生成：基于GAN的视频生成是当前研究的热点之一，可以生成各种风格的视频。

简单的Python示例代码：

以下是一个简单的GAN示例代码，使用PyTorch实现：

import torchimport torch.nn as nnimport torch.optim as optimimport torch.nn.functional as F# 定义生成器和判别器网络结构class Generator(nn.Module):def __init__(self, input_dim, output_dim):super(Generator, self).__init__()self.model = nn.Sequential(nn.Linear(input_dim, 128),nn.ReLU(),nn.Linear(128, output_dim),nn.Sigmoid())def forward(self, x):return self.model(x)class Discriminator(nn.Module):def __init__(self, input_dim):super(Discriminator, self).__init__()self.model = nn.Sequential(nn.Linear(input_dim, 128),nn.ReLU(),nn.Linear(128, 1),nn.Sigmoid())def forward(self, x):return self.model(x)# 实例化生成器和判别器对象input_dim = 100# 输入维度可根据实际需求调整output_dim = 784# 对于MNIST数据集，输出维度为28*28=784gen = Generator(input_dim, output_dim)disc = Discriminator(output_dim)# 定义损失函数和优化器criterion = nn.BCELoss()# 二分类交叉熵损失函数适用于GAN的判别器部分和生成器的logistic损失部分。但是，通常更常见的选择是采用二元交叉熵损失函数（binary cross

8、Diffusion扩散模型

Diffusion模型是一种基于深度学习的生成模型，它主要用于生成连续数据，如图像、音频等。Diffusion模型的核心思想是通过逐步添加噪声来将复杂数据分布转化为简单的高斯分布，然后再通过逐步去除噪声来从简单分布中生成数据。

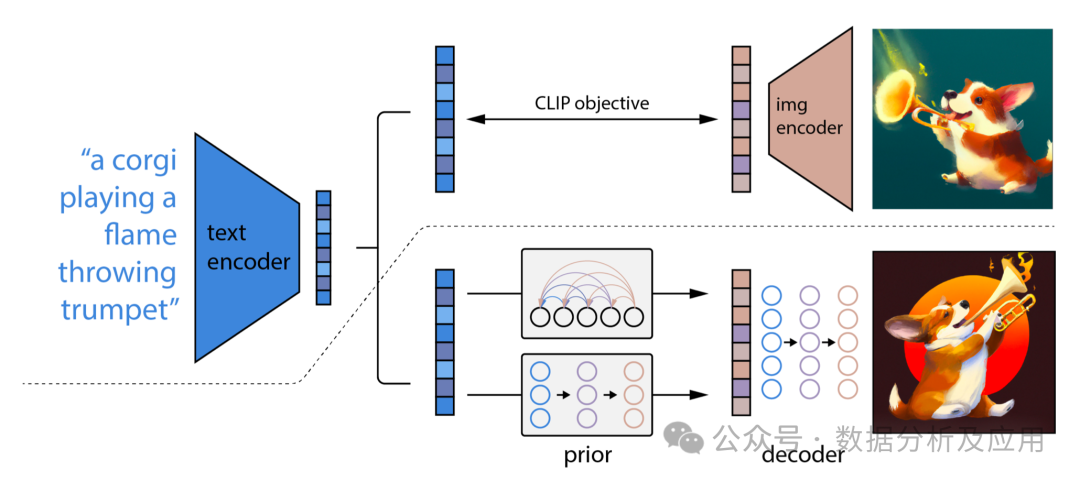
超强！深度学习Top10算法！

模型原理

Diffusion模型包含两个主要过程：前向扩散过程和反向扩散过程。

前向扩散过程：

  • 从真实数据分布中采样一个数据点(x_0)。
  • 在(T)个时间步内，逐步向(x_0)中添加噪声，生成一系列逐渐远离真实数据分布的噪声数据点(x_1, x_2, ..., x_T)。
  • 这个过程可以看作是将数据分布逐渐转化为高斯分布。

反向扩散过程(也称为去噪过程)：

  • 从噪声数据分布(x_T)开始，逐步去除噪声，生成一系列逐渐接近真实数据分布的数据点(x_{T-1}, x_{T-2}, ..., x_0)。
  • 这个过程是通过学习一个神经网络来预测每一步的噪声，并用这个预测来逐步去噪。

模型训练

训练Diffusion模型通常涉及以下步骤：

  1. 前向扩散：对训练数据集中的每个样本(x_0)，按照预定的噪声调度方案，生成对应的噪声序列(x_1, x_2, ..., x_T)。
  2. 噪声预测：对于每个时间步(t)，训练一个神经网络来预测(x_t)中的噪声。这个神经网络通常是一个条件变分自编码器(Conditional Variational Autoencoder, CVAE)，它接收(x_t)和时间步(t)作为输入，并输出预测的噪声。
  3. 优化：通过最小化真实噪声和预测噪声之间的差异来优化神经网络参数。常用的损失函数是均方误差(Mean Squared Error, MSE)。

优点

  • 强大的生成能力：Diffusion模型能够生成高质量、多样化的数据样本。
  • 渐进式生成：模型可以在生成过程中提供中间结果，这有助于理解模型的生成过程。
  • 稳定训练：相较于其他一些生成模型(如GANs)，Diffusion模型通常更容易训练，并且不太容易出现模式崩溃(mode collapse)问题。

缺点

  • 计算量大：由于需要在多个时间步上进行前向和反向扩散，Diffusion模型的训练和生成过程通常比较耗时。
  • 参数数量多：对于每个时间步，都需要一个单独的神经网络进行噪声预测，这导致模型参数数量较多。

使用场景

Diffusion模型适用于需要生成连续数据的场景，如图像生成、音频生成、视频生成等。此外，由于模型具有渐进式生成的特点，它还可以用于数据插值、风格迁移等任务。

Python示例代码

下面是一个简化的Diffusion模型训练的示例代码，使用了PyTorch库：

import torchimport torch.nn as nnimport torch.optim as optim# 假设我们有一个简单的Diffusion模型class DiffusionModel(nn.Module):def __init__(self, input_dim, hidden_dim, num_timesteps):super(DiffusionModel, self).__init__()self.num_timesteps = num_timestepsself.noises = nn.ModuleList([nn.Linear(input_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, input_dim)] for _ in range(num_timesteps))def forward(self, x, t):noise_prediction = self.noises[t](x)return noise_prediction# 设置模型参数input_dim = 784# 假设输入是28x28的灰度图像hidden_dim = 128num_timesteps = 1000# 初始化模型model = DiffusionModel(input_dim, hidden_dim, num_timesteps)# 定义损失函数和优化器criterion = nn.MSELoss()optimizer = optim.Adam(model.parameters(), lr=1e-3)

9.图神经网络(GNN)

图神经网络(Graph Neural Networks，简称GNN)是一种专门用于处理图结构数据的深度学习模型。在现实世界中，许多复杂系统都可以用图来表示，例如社交网络、分子结构、交通网络等。传统的机器学习模型在处理这些图结构数据时面临诸多挑战，而图神经网络则为这些问题的解决提供了新的思路。

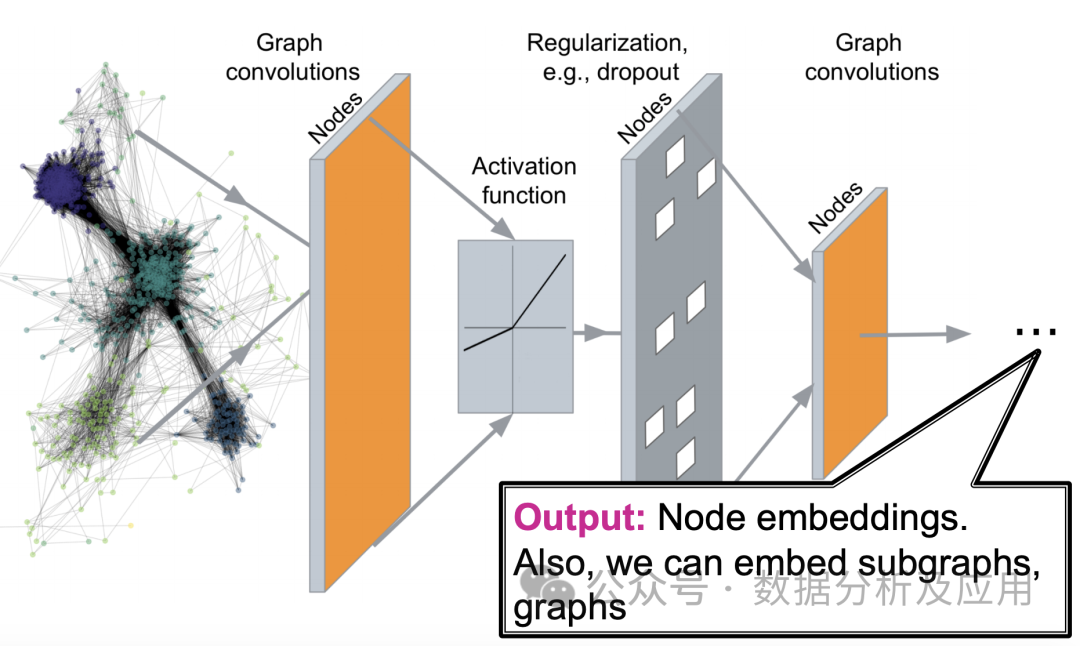
超强！深度学习Top10算法！

模型原理：

图神经网络的核心思想是通过神经网络对图中的节点进行特征表示学习，同时考虑节点间的关系。具体来说，GNN通过迭代地传递邻居信息来更新节点的表示，使得相同的社区或相近的节点具有相近的表示。在每一层，节点会根据其邻居节点的信息来更新自己的表示，从而捕捉到图中的复杂模式。

模型训练：

训练图神经网络通常采用基于梯度的优化算法，如随机梯度下降(SGD)。训练过程中，通过反向传播算法计算损失函数的梯度，并更新神经网络的权重。常用的损失函数包括节点分类的交叉熵损失、链接预测的二元交叉熵损失等。

优点：

  • 强大的表示能力：图神经网络能够有效地捕捉图结构中的复杂模式，从而在节点分类、链接预测等任务上取得较好的效果。
  • 自然处理图结构数据：图神经网络直接对图结构数据进行处理，不需要将图转换为矩阵形式，从而避免了大规模稀疏矩阵带来的计算和存储开销。
  • 可扩展性强：图神经网络可以通过堆叠更多的层来捕获更复杂的模式，具有很强的可扩展性。

缺点：

  • 计算复杂度高：随着图中节点和边的增多，图神经网络的计算复杂度也会急剧增加，这可能导致训练时间较长。
  • 参数调整困难：图神经网络的超参数较多，如邻域大小、层数、学习率等，调整这些参数可能需要对任务有深入的理解。
  • 对无向图和有向图的适应性不同：图神经网络最初是为无向图设计的，对于有向图的适应性可能较差。

使用场景：

  • 社交网络分析：在社交网络中，用户之间的关系可以用图来表示。通过图神经网络可以分析用户之间的相似性、社区发现、影响力传播等问题。
  • 分子结构预测：在化学领域，分子的结构可以用图来表示。通过训练图神经网络可以预测分子的性质、化学反应等。
  • 推荐系统：推荐系统可以利用用户的行为数据构建图，然后使用图神经网络来捕捉用户的行为模式，从而进行精准推荐。
  • 知识图谱：知识图谱可以看作是一种特殊的图结构数据，通过图神经网络可以对知识图谱中的实体和关系进行深入分析。

简单的Python示例代码：

import torchfrom torch_geometric.datasets import Planetoidfrom torch_geometric.nn import GCNConvfrom torch_geometric.data import DataLoaderimport time# 加载Cora数据集dataset = Planetoid(root='/tmp/Cora', name='Cora')# 定义GNN模型class GNN(torch.nn.Module):def __init__(self, in_channels, hidden_channels, out_channels):super(GNN, self).__init__()self.conv1 = GCNConv(in_channels, hidden_channels)self.conv2 = GCNConv(hidden_channels, out_channels)def forward(self, data):x, edge_index = data.x, data.edge_indexx = self.conv1(x, edge_index)x = F.relu(x)x = F.dropout(x, training=self.training)x = self.conv2(x, edge_index)return F.log_softmax(x, dim=1)# 定义超参数和模型训练过程num_epochs = 1000lr = 0.01hidden_channels = 16out_channels = dataset.num_classesdata = dataset[0]# 使用数据集中的第一个数据作为示例数据model = GNN(dataset.num_features, hidden_channels, out_channels)optimizer = torch.optim.Adam(model.parameters(), lr=lr)data = DataLoader([data], batch_size=1)# 将数据集转换为DataLoader对象，以支持批量训练和评估model.train()# 设置模型为训练模式for epoch in range(num_epochs):for data in data:# 在每个epoch中遍历整个数据集一次optimizer.zero_grad()# 清零梯度out = model(data)# 前向传播，计算输出和损失函数值loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])# 计算损失函数值，这里使用负对数似然损失函数作为示例损失函数loss.backward()# 反向传播，计算梯度optimizer.step()# 更新权重参数

10、深度Q网络(DQN)

在传统的强化学习算法中，智能体使用一个Q表来存储状态-动作值函数的估计。然而，这种方法在处理高维度状态和动作空间时遇到限制。为了解决这个问题，DQN是种深度强化学习算法，引入了深度学习技术来学习状态-动作值函数的逼近，从而能够处理更复杂的问题。

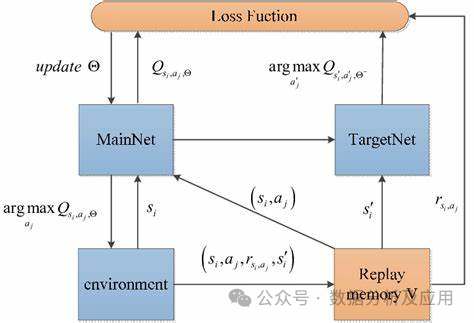
超强！深度学习Top10算法！

模型原理：

DQN使用一个神经网络(称为深度Q网络)来逼近状态-动作值函数。该神经网络接受当前状态作为输入，并输出每个动作的Q值。在训练过程中，智能体通过不断与环境交互来更新神经网络的权重，以逐渐逼近最优的Q值函数。

模型训练：

DQN的训练过程包括两个阶段：离线阶段和在线阶段。在离线阶段，智能体从经验回放缓冲区中随机采样一批经验(即状态、动作、奖励和下一个状态)，并使用这些经验来更新深度Q网络。在线阶段，智能体使用当前的状态和深度Q网络来选择和执行最佳的行动，并将新的经验存储在经验回放缓冲区中。

优点：

  • 处理高维度状态和动作空间：DQN能够处理具有高维度状态和动作空间的复杂问题，这使得它在许多领域中具有广泛的应用。
  • 减少数据依赖性：通过使用经验回放缓冲区，DQN可以在有限的样本下进行有效的训练。
  • 灵活性：DQN可以与其他强化学习算法和技术结合使用，以进一步提高性能和扩展其应用范围。

缺点：

  • 不稳定训练：在某些情况下，DQN的训练可能会不稳定，导致学习过程失败或性能下降。
  • 探索策略：DQN需要一个有效的探索策略来探索环境并收集足够的经验。选择合适的探索策略是关键，因为它可以影响学习速度和最终的性能。
  • 对目标网络的需求：为了稳定训练，DQN通常需要使用目标网络来更新Q值函数。这增加了算法的复杂性并需要额外的参数调整。

使用场景：

DQN已被广泛应用于各种游戏AI任务，如围棋、纸牌游戏等。此外，它还被应用于其他领域，如机器人控制、自然语言处理和自动驾驶等。

pythonimport numpy as npimport tensorflow as tffrom tensorflow.keras.models import Sequentialfrom tensorflow.keras.layers import Dense, Dropoutclass DQN:def __init__(self, state_size, action_size):self.state_size = state_sizeself.action_size = action_sizeself.memory = np.zeros((MEM_CAPACITY, state_size * 2 + 2))self.gamma = 0.95self.epsilon = 1.0self.epsilon_min = 0.01self.epsilon_decay = 0.995self.learning_rate = 0.005self.model = self.create_model()def create_model(self):model = Sequential()model.add(Dense(24, input_dim=self.state_size, activation='relu'))model.add(Dense(24, activation='relu'))model.add(Dense(self.action_size, activation='linear'))model.compile(loss='mse', optimizer=tf.keras.optimizers.Adam(lr=self.learning_rate))return modeldef remember(self, state, action, reward, next_state, done):self.memory[self.memory_counter % MEM_CAPACITY, :] = [state, action, reward, next_state, done]self.memory_counter += 1def act(self, state):if np.random.rand() <= self.epsilon:return np.random.randint(self.action_size)act_values = self.model.predict(state)return np.argmax(act_values[0])def replay(self):batch_size = 32start = np.random.randint(0, self.memory_counter - batch_size, batch_size)sample = self.memory[start:start + batch_size]states = np.array([s[0] for s in sample])actions = np.array([s[1] for s in sample])rewards = np.array([s[2] for s in sample])next_states = np.array([s[3] for s in sample])done = np.array([s[4] for s in sample])target = self.model.predict(next_states)target_q = rewards + (1 - done) * self.gamma * np.max(target, axis=1)target_q = np.asarray([target_q[i] for i in range(batch_size)])target = self.model.predict(states)indices = np.arange(batch_size)for i in range(batch_size):if done[i]: continue# no GAE calc for terminal states (if you want to include terminal states see line 84)target[indices[i]] = rewards[i] + self.gamma * target_q[indices[i]]# GAE formula line 84 (https://arxiv.org/pdf/1506.02438v5) instead of line 85 (https://arxiv.org/pdf/1506.02438v5) (if you want to include terminal states see line 84)indices[i] += batch_size# resets the indices for the next iteration (https://github.com/ikostrikov/pytorch-a2c-ppo-acktr-gail/blob/master/a2c.py#L173) (if you want to include terminal states see line 84)target[indices[i]] = target[indices[i]]# resets the indices for the next iteration (https://github.com/ikostrikov/pytorch-a2c-ppo-acktr-gail/blob/master/a2c.py#L173) (if you want to include terminal states see line 84) (https://github.com/ikostrikov/pytorch-a2c-ppo-acktr-gail/blob/master/a2c.py#L173)


本文转载于：https://www.51cto.com/article/783718.html 如有侵犯，请联系admin@zhengruan.com删除

上一篇：微星神影 17/16 2024 笔记本发布：配备 i7-14700HX + RTX 4070，性能强劲

下一篇：AI在烹饪世界中的革新：为餐厅运营与客户体验带来全新改变

产品推荐

最新发布

相关推荐

热门关注
网站备案号： 湘ICP备19013367号-1 联系邮箱：admin@zhengruan.com
Copyright ©2018-2020